
分析 根据终边相同的角的概念,写出与所求角的终边相同的角的集合S,再求出S中适合条件的元素α即可.
解答 解:(1)①与60°角终边相同的角的集合为S={α|α=60°+k•360°,k∈Z},
当k=-1时,α=-300°,k=0时,α=60°,k=1,α=420°;
∴S中适合不等式-360°≤α<720°的元素α为:-300°,60°,420°;
②与-21°角终边相同的角的集合为S={α|α=-21°+k•360°,k∈Z},
当k=0时,α=-21°,k=1时,α=339°,k=2时,α=699°;
∴S中适合不等式-360°≤α<720°的元素α为:-21°,339°,699°;
(2)直线y=-$\sqrt{3}$x的斜率为k=-$\sqrt{3}$,倾斜角为β=120°,
∴终边在直线y=-$\sqrt{3}$x上的角的集合为S={α|α=120°+k•180°,k∈Z},
当k=-1时,α=-60°,k=0时,α=120°;
∴S中适合不等式-180°≤α<180°的元素α为-60°,120°.
点评 本题考查了与已知角终边相同的角的概念的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2n-1 | C. | n2 | D. | 2n2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{6}{5}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
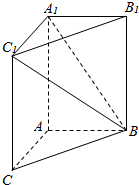 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com