
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先求函数导数,转化为研究导函数零点,即方程![]() =0的根的情况,当
=0的根的情况,当![]() ,导函数不变号,在
,导函数不变号,在![]() 上单调递减,当
上单调递减,当![]() 时,有两个不等根,列表分析导函数符号变化规律,确定对应单调区间,(2)(i)利用导数几何意义化简条件:
时,有两个不等根,列表分析导函数符号变化规律,确定对应单调区间,(2)(i)利用导数几何意义化简条件: ![]() 在
在![]() ,
, ![]() 处的切线相互垂直,得
处的切线相互垂直,得![]() ,利用基本不等式证明不等式,(ii)先分别求出切线方程,再根据切线重合得
,利用基本不等式证明不等式,(ii)先分别求出切线方程,再根据切线重合得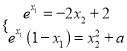 ,消元
,消元![]() 得
得![]() ,利用导数研究函数
,利用导数研究函数![]() ,
, ![]() 单调性,确定函数
单调性,确定函数![]() 值域,进而确定
值域,进而确定![]() 的取值范围.
的取值范围.
试题解析:解:(1)![]() ,则
,则![]() ,
,
当![]() 即
即![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时即
时即![]() 时,
时, ![]() ,
,
此时![]() 在
在![]() 和
和![]() 上都是单调递减的,在
上都是单调递减的,在![]() 上是单调递增的;
上是单调递增的;
(2)(i)![]() ,据题意有
,据题意有![]() ,又
,又![]() ,
,
则![]() 且
且![]() ,
, ![]() ,
,
法1: ![]() ,
,
当且仅当![]() 即
即![]() ,
, ![]() 时取等号.
时取等号.
法2: ![]() ,
, 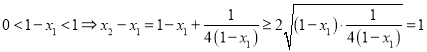 ,
,
当且仅当![]() 时取等号.
时取等号.
(ii)要在点![]() 处的切线重合,首先需要在点
处的切线重合,首先需要在点![]() 处的切线的斜率相等,
处的切线的斜率相等,
而![]() 时,
时, ![]() ,则必有
,则必有![]() ,即
,即![]() ,
, ![]() ,
,
![]() 处的切线方程是:
处的切线方程是: ![]()
![]() 处的切线方程是:
处的切线方程是: ![]() ,
,
即![]() ,
,
据题意则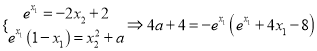 ,
, ![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,
, ![]() 在
在![]() 上恒成立,
上恒成立,
则![]() 在
在![]() 上单调递增
上单调递增![]() ,
,
则![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,再设
,再设![]() ,
, ![]() ,
,
![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,
则![]() 在
在![]() 恒成立,
恒成立,
即当![]() 时,
时, ![]() 的值域是
的值域是![]() ,
,
故![]() ,即为所求.
,即为所求.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距 ![]() km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 和圆
和圆![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
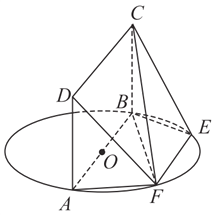
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中: ①|BM|是定值;
②点M在圆上运动;
③一定存在某个位置,使DE⊥A1C;
④一定存在某个位置,使MB∥平面A1DE.
其中正确的命题是( )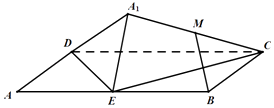
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x+1)的定义域是[﹣1,3],则y=f(x2)的定义域是( )
A.[0,4]
B.[0,16]
C.[﹣2,2]
D.[1,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣σ<X≤μ+σ)=0.6826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.1358
B.0.1359
C.0.2716
D.0.2718
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com