
【题目】如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中: ①|BM|是定值;
②点M在圆上运动;
③一定存在某个位置,使DE⊥A1C;
④一定存在某个位置,使MB∥平面A1DE.
其中正确的命题是( )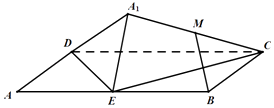
A.①②③
B.①②④
C.①③④
D.②③④
【答案】B
【解析】解:取CD中点F,连接MF,BF,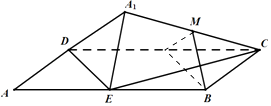
则MF∥DA1 , BF∥DE,∴平面MBF∥平面A1DE,∴MB∥平面A1DE,故④正确
由∠A1DE=∠MFB,MF= ![]() A1D=定值,FB=DE=定值,
A1D=定值,FB=DE=定值,
由余弦定理可得MB2=MF2+FB2﹣2MFFBcos∠MFB,所以MB是定值,故①正确.
∵B是定点,∴M是在以B为圆心,MB为半径的圆上,故②正确,
∵A1C在平面ABCD中的射影为AC,AC与DE不垂直,
∴存在某个位置,使DE⊥A1C不正确,故③不正确.
故选:B.
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案,需要熟知两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知实数a,b,则“a>b”是“a2>b2”的必要不充分条件
B.“存在x0∈R,使得 ![]() ”的否定是“对任意x∈R,均有x2﹣1>0”
”的否定是“对任意x∈R,均有x2﹣1>0”
C.函数 ![]() 的零点在区间
的零点在区间 ![]() 内
内
D.设m,n是两条直线,α,β是空间中两个平面,若m?α,n?β,m⊥n,则α⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() cos2x+sin2(x+
cos2x+sin2(x+ ![]() ). (Ⅰ)求f(x)的最小正周期和单调递增区间;
). (Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈[﹣ ![]() ,
, ![]() )时,求f(x)的取值范围.
)时,求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点. 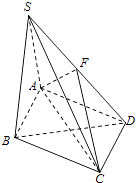
(1)求三棱锥S﹣FAC的体积;
(2)求直线BD与平面FAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() 的离心率为
的离心率为 ![]() ,焦距为
,焦距为 ![]() ,抛物线C2:x2=2py(p>0)的焦点F是椭圆C1的顶点. (Ⅰ)求C1与C2的标准方程;
,抛物线C2:x2=2py(p>0)的焦点F是椭圆C1的顶点. (Ⅰ)求C1与C2的标准方程;
(Ⅱ)C1上不同于F的两点P,Q满足 ![]() ,且直线PQ与C2相切,求△FPQ的面积.
,且直线PQ与C2相切,求△FPQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学校本课程开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生.
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子中装有三个编号分别为1,2,3的红球和三个编号分别为1,2,3的白球,三个红球按其编号分别记为a1 , a2 , a3 , 三个白球按其编号分别记为b1 , b2 , b3 , 袋中的6个球除颜色和编号外没有任何差异,现从袋中一次随机地取出两个球,
(1)列举所有的基本事件,并写出其个数;
(2)规定取出的红球按其编号记分,取出的白球按其编号的2倍记分,取出的两个球的记分之和为一次取球的得分,求一次取球的得分不小于6的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com