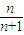练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对集合A，如果存在x使得对任意正数a，都存在x∈A，使0＜|x-x|＜a，则称x为集合A的“聚点”，给出下列四个集合：
    ①；
    ②{x∈R|x≠0}；
    ③；
    ④Z．
    其中以0为“聚点”的集合是（ ）
    A．②③
    B．①②
    C．①③
    D．②④
    【答案】分析：利用“聚点”的定义可得①的聚点是1，②的聚点是0，③的聚点是0，而④无聚点．
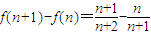    解答：解：①令f（n）=，则=，即f（n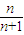）=当n∈N时单调递增，则1为其“聚点”，下面给出证明：
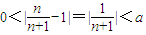    取x=1，对任意正数a，要使成立，只要取正整数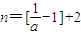，故1是其“聚点”；
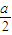    ②由实数的稠密性可知：对任意正数a，都存在x=∈{x∈R|x≠0}，使0＜|x-0|＜a成立，故0是此集合的“聚点”；
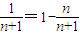    ③∵，由（1）可知：0为集合{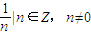}，根据“聚点”的定义可知，0是其聚点；
    ④?n∈Z，且n≠0，则|n|≥1，故取0＜a＜1，则不存在x∈Z，使0＜|x-x|＜a成立，根据“聚点”的定义可知：所给集合不存在聚点．
    综上可知：只有②③正确；
    故选A．
    点评：正确理解函数的单调性、实数的稠密性、聚点的定义是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•湛江二模）对集合A，如果存在x0使得对任意正数a，都存在x∈A，使0＜|x-x0|＜a，则称x0为集合A的“聚点”，给出下列四个集合：
    ①{
    n
    n+1
    |n∈Z，n≥0}    ；
    ②{x∈R|x≠0}；
    ③{
    1
    n
    |n∈Z，n≠0}    ；
    ④Z．
    其中以0为“聚点”的集合是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    对集合A，如果存在x0使得对任意正数a，都存在x∈A，使0＜|x-x0|＜a，则称x0为集合A的“聚点”，给出下列四个集合：
    ①{
    n
    n+1
    |n∈Z，n≥0}    ；
    ②{x∈R|x≠0}；
    ③{
    1
    n
    |n∈Z，n≠0}    ；
    ④Z．
    其中以0为“聚点”的集合是（　　）
    A．②③B．①②C．①③D．②④

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江苏省连云港市东海县高级中学高三（上）期末数学模拟试卷（一）（解析版） 题型：解答题

    A是定义在[2，4]上且满足如下两个条件的函数Φ（x）组成的集合：
    ①对任意的x∈[1，2]，都有Φ（2x）∈（1，2）；
    ②存在常数L（0＜L＜1），使得对任意的x1，x2∈[1，2]，都有|Φ（2x1）-Φ（2x2）|≤L|x1-x2|；
    （1）设，证明：Φ（x）∈A；
    （2）设Φ（x）∈A，如果存在x∈（1，2），使得x=Φ（2x），那么，这样的x是唯一的；
    （3）设Φ（x）∈A，任取x1∈（1，2），令xn+1=Φ（2xn），n=1，2，…，
    证明：给定正整数k，对任意的正整数p，不等式成立．

    查看答案和解析>>

    科目：高中数学 来源：2013年北京市延庆县高考数学一模试卷（文科）（解析版） 题型：解答题

    A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
    （1）对任意x∈[1，2]，都有φ（2x）∈（1，2）；
    （2）存在常数L（0＜L＜1），使得对任意的x1，x2∈[1，2]，都有|φ（2x1）-φ（2x2）|≤L|x1-x2|．
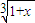    （Ⅰ）设φ（x）=，x∈[1，2]，证明：φ（x）∈A；
    （Ⅱ）设φ（x）∈A，如果存在x∈（1，2），使得x=φ（2x），那么这样的x是唯一的．

    查看答案和解析>>

    同步练习册答案