
| A. | (-∞,-3)∪(0,3) | B. | (-∞,-3)∪(3,+∞) | C. | (-3,0)∪(0,3) | D. | (-3,0)∪(3,+∞) |
分析 构造函数g(x)=$\frac{f(x)}{x}$,求函数的导数,以及函数的单调性,结合函数奇偶性和单调性的关系将不等式f(x)>0转化为g(x)>0或g(x)<0进行求解即可.
解答  解:设g(x)=$\frac{f(x)}{x}$,
解:设g(x)=$\frac{f(x)}{x}$,
则g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵当x>0时,有f(x)-xf′(x)>0成立,
∴当x>0时,有xf′(x)-f(x)<0成立,即此时g′(x)<0,函数g(x)为减函数,
∵f(x)是定义在R上的奇函数且f(-3)=0,
∴f(3)=0,且g(x)是偶函数,g(3)=g(-3)=0
当x>0时,f(x)>0等价为g(x)>0,即g(x)>g(3),得0<x<3,
当x<0时,f(x)>0等价为g(x)<0,即g(x)<g(-3),
此时函数g(x)增函数,得x<-3,
综上不等式f(x)>0的解集是(-∞,-3)∪(0,3),
故选:A.
点评 本题主要考查不等式的求解,根据条件构造函数,求函数的导数,利用导数研究函数的单调性,结合函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.综合性较强.


科目:高中数学 来源: 题型:选择题
| A. | 至多抽到2件次品 | B. | 至多抽到2件正品 | C. | 至少抽到2件正品 | D. | 至多抽到1件次品 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=sin(ωx+ϕ)(ω>0)的部分图象如图所示,下面结论正确的个数是( )
已知函数f(x)=sin(ωx+ϕ)(ω>0)的部分图象如图所示,下面结论正确的个数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
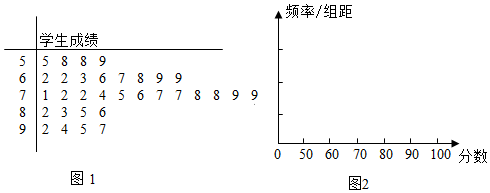
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是绵阳市某小区100户居民2014年平均用水量(单位:t)的频率分布直方图,则该小区2014年的月平均用水量的众数,中位数的估计值分别是( )
如图是绵阳市某小区100户居民2014年平均用水量(单位:t)的频率分布直方图,则该小区2014年的月平均用水量的众数,中位数的估计值分别是( )| A. | 2,2.5 | B. | 2,2.02 | C. | 2.25,2.5 | D. | 2.25,2.02 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com