
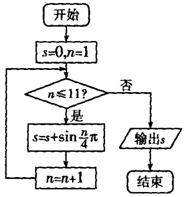
分析 题目给出了当型循环结构框图,首先引入累加变量s和循环变量n,由判断框得知,算法执行的是求$\frac{nπ}{4}$的正弦值的和,n从1取到11.
解答 解:通过分析知该算法是求和sin$\frac{π}{4}$+sin$\frac{2π}{4}$+sin$\frac{3π}{4}$+…+sin $\frac{11π}{4}$,
在该和式中,从第一项起,前8项和为0,
故sin$\frac{9π}{4}$+sin$\frac{10π}{4}$+sin$\frac{11π}{4}$=sin$\frac{π}{4}$+sin$\frac{2π}{4}$+sin$\frac{3π}{4}$=1+$\sqrt{2}$.
故答案为:1+$\sqrt{2}$.
点评 本题考查了程序框图中的当型循环结构,当型循环结构是先判断再执行,若满足条件进入循环,否则结束循环,循环结构主要用在一些规律的重复计算,如累加、累积等,在循环结构中框图中,特别要注意条件应用,如计数变量和累加变量等.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{12}-\frac{y^2}{24}=1$ | B. | $\frac{y^2}{12}-\frac{x^2}{24}=1$ | C. | $\frac{y^2}{24}-\frac{x^2}{12}=1$ | D. | $\frac{x^2}{24}-\frac{y^2}{12}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
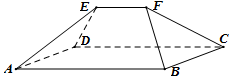 《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )| A. | $8\sqrt{3}$ | B. | $8+8\sqrt{3}$ | C. | $6\sqrt{2}+2\sqrt{3}$ | D. | $8+6\sqrt{2}+2\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com