
Ζ÷Έω …η$\overrightarrow a=2\overrightarrow{e_1}+\overrightarrow{e_2}$”κ$\overrightarrow b=-3\overrightarrow{e_1}+2\overrightarrow{e_2}$ΒΡΦ–Ϋ«ΈΣΠ»Θ§άϊ”ΟΝΫΗωœρΝΩΒΡ ΐΝΩΜΐΒΡΕ®“εΘ§ΝΫΗωœρΝΩΒΡΦ–Ϋ«ΙΪ Ϋ«σΒΟcosΠ»ΒΡ÷ΒΘ§Ω…ΒΟsinΠ» ΒΡ÷ΒΘ°
Ϋβ¥π ΫβΘΚ”…Χβ“βΩ…ΒΟ$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=1ΓΝ1ΓΝcos60Γψ=$\frac{1}{2}$Θ§…η$\overrightarrow a=2\overrightarrow{e_1}+\overrightarrow{e_2}$”κ$\overrightarrow b=-3\overrightarrow{e_1}+2\overrightarrow{e_2}$ΒΡΦ–Ϋ«ΈΣΠ»Θ§
‘ρ$\overrightarrow{a}•\overrightarrow{b}$=-6${\overrightarrow{{e}_{1}}}^{2}$+$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$+2${\overrightarrow{{e}_{2}}}^{2}$=-6+$\frac{1}{2}$+2=-$\frac{7}{2}$Θ§
|$\overrightarrow{a}$|=$\sqrt{{Θ®2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}Θ©}^{2}}$=$\sqrt{4+4ΓΝ\frac{1}{2}+1}$=$\sqrt{7}$Θ§|$\overrightarrow{b}$|=$\sqrt{{Θ®-3\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}}Θ©}^{2}}$=$\sqrt{9-12ΓΝ\frac{1}{2}+4}$=$\sqrt{7}$Θ§
ΓύcosΠ»=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-\frac{7}{2}}{\sqrt{7}•\sqrt{7}}$=-$\frac{1}{2}$Θ§ΓύΠ»=$\frac{2Π–}{3}$Θ§ΓύsinΠ»=$\sqrt{{1-cos}^{2}Π»}$=$\frac{\sqrt{3}}{2}$Θ§
Ι ¥πΑΗΈΣΘΚ$\frac{{\sqrt{3}}}{2}$Θ°
ΒψΤά ±ΨΧβ÷ς“ΣΩΦ≤ιΝΫΗωœρΝΩΒΡ ΐΝΩΜΐΒΡΕ®“εΘ§ΝΫΗωœρΝΩΒΡΦ–Ϋ«ΙΪ ΫΒΡ”Π”ΟΘ§ τ”Ύ÷–ΒΒΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ’ψΫ≠Έά ”ΓΑ±Φ≈ήΑ…–÷ΒήΓ±Ήέ“’ΫΎΡΩΒΡ ’ ”¬ Θ§≤…”Ο≥ι≤ιΒΡΖΫ Ϋ | |
| BΘ° | ΝΥΫβΡ≥”φ≥Γ÷–«ύ”ψΒΡΤΫΨυ÷ΊΝΩΘ§≤…”Ο≥ι≤ιΒΡΖΫ Ϋ | |
| CΘ° | ΝΥΫβiphone6s ÷ΜζΒΡ Ι”Ο ΌΟϋΘ§≤…”ΟΤ’≤ιΒΡΖΫ Ϋ | |
| DΘ° | ΝΥΫβ“Μ≈ζΤϊ≥ΒΒΡ…≤≥Β–‘ΡήΘ§≤…”ΟΤ’≤ιΒΡΖΫ Ϋ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\sqrt{2}$ | BΘ° | $\sqrt{3}$ | CΘ° | $\sqrt{5}$ | DΘ° | 5 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
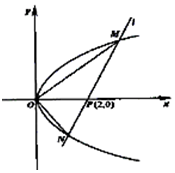 »γΆΦΘ§OΈΣΉχ±ξ‘≠ΒψΘ§ΙΐΒψPΘ®2Θ§0Θ©«“–±¬ ΈΣkΒΡ÷±œΏlΫΜ≈ΉΈοœΏy2=2x”ΎMΘ®x1Θ§y1Θ©Θ§NΘ®x2Θ§y2Θ©ΝΫΒψΘ°
»γΆΦΘ§OΈΣΉχ±ξ‘≠ΒψΘ§ΙΐΒψPΘ®2Θ§0Θ©«“–±¬ ΈΣkΒΡ÷±œΏlΫΜ≈ΉΈοœΏy2=2x”ΎMΘ®x1Θ§y1Θ©Θ§NΘ®x2Θ§y2Θ©ΝΫΒψΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | y=x+1 | BΘ° | y=$\frac{1}{x}$ | CΘ° | y=x2 | DΘ° | y=x5 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | aΘΦbΘΦc | BΘ° | cΘΦbΘΦa | CΘ° | aΘΦcΘΦb | DΘ° | cΘΦaΘΦb |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| AΘ° | 9400 | BΘ° | 9408 | CΘ° | 9410 | DΘ° | 9414 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com