
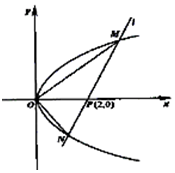
 如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.分析 (1)由题意可知:直线方程为:y=x-2,代入抛物线方程,由韦达定理可知:x1+x2=6,x1x2=4,则弦长公式可知|MN|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,即可求得|MN|;
(2)设直线方程方程,y=k(x-2)(k≠0),代入抛物线方程,即可求得x1x2=4,则(y1y2)2=4x1x2,则求得y1y2,则由斜率公式可知:k1•k2=$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{1}}{{x}_{1}}$=-1,即可证明OM⊥ON.
解答 解:(1)由题意可知:直线方程为:y=x-2,
则$\left\{\begin{array}{l}{{y}^{2}=2x}\\{y=x-2}\end{array}\right.$,整理得:x2-6x+4=0,
由韦达定理可知:x1+x2=6,x1x2=4,
∴|MN|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{36-4×4}$=2$\sqrt{10}$,
∴|MN|=2$\sqrt{10}$;
(2)证明:直线l过点P(2,0)且斜率为k,设直线l的方程为y=k(x-2)(k≠0)
∴$\left\{\begin{array}{l}{y=k(x-2)}\\{{y}^{2}=2x}\end{array}\right.$,消去y代入可得k2x2-2(k2+1)x+4k2=0.
由韦达定理可知:x1x2=$\frac{4{k}^{2}}{{k}^{2}}$=4,
由y12=2x1,y22=2x2,则(y1y2)2=4x1x2=4×4=16,
又注意到y1y2<0,
所以y1y2=-4.
设OM,ON的斜率分别为k1,k2,
则k1=$\frac{{y}_{1}}{{x}_{1}}$,k2=$\frac{{y}_{1}}{{x}_{1}}$,
k1•k2=$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{1}}{{x}_{1}}$=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-4}{4}$=-1,
∴OM⊥ON.
点评 本题考查抛物线的标准方程,直线与抛物线的位置关系,考查韦达定理,弦长公式及直线直线的斜率公式,考查计算能力,属于中档题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}i$ | D. | $\frac{4}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{3}$或$\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (0,4) | C. | (-1,$\frac{7}{2}$) | D. | (-1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于z轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于平面xOy对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,${x_0}^2+1≤0$ | B. | ?x0∈R,${x_0}^2+1>0$ | C. | ?x0∈R,${x_0}^2+1<0$ | D. | ?x0∈R,${x_0}^2+1≤0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com