
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{3}$或$\frac{5π}{3}$ |
分析 直线$\left\{\begin{array}{l}{x=4+at}\\{y=bt}\end{array}\right.$ 的普通方程是y=k(x-4),k=$\frac{b}{a}$,x2+y2-4x+1=0的标准方程是(x-2)2+y2=3,由直线与圆相切知,$\frac{|2k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{3}$,求出k,从而求得直线的倾斜角α,
解答 解:直线$\left\{\begin{array}{l}{x=4+at}\\{y=bt}\end{array}\right.$ 的普通方程是y=k(x-4),
k=$\frac{b}{a}$,x2+y2-4x+1=0的标准方程是(x-2)2+y2=3
由直线与圆相切知,$\frac{|2k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{3}$,∴k=$±\sqrt{3}$,
因直线的倾斜角α∈[0,π),
则α=$\frac{π}{3}$或$\frac{2π}{3}$.
故选C.
点评 本小题主要考查直线的方程、圆的参数方程、考查运算求解能力.属于基础题.本题体现了化归思想,化不熟悉为熟悉


科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [-3,0) | C. | [-2,0) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,2} | C. | {-2,-1} | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20π | B. | 42π | C. | 52π | D. | 56π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -e | B. | -$\frac{1}{e}$ | C. | e | D. | $\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
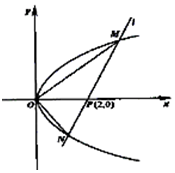 如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
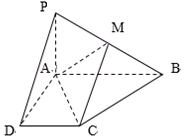 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M为PB中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M为PB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com