
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域上是单调增函数,求实数a的取值范围;
在定义域上是单调增函数,求实数a的取值范围;
(2)讨论![]() 的极值点的个数;
的极值点的个数;
(3)若![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的极值点的个数为0;当
的极值点的个数为0;当![]() 时,
时,![]() 的极值点的个数为2;(3)
的极值点的个数为2;(3)![]()
【解析】
(1)求出导函数![]() ,题意说明
,题意说明![]() 在
在![]() 上恒成立,可用分离参数法转化为求函数最值(可用基本不等式求最值).
上恒成立,可用分离参数法转化为求函数最值(可用基本不等式求最值).
(2)由![]() ,对
,对![]() 分类讨论,在(1)的基础上,
分类讨论,在(1)的基础上,![]() 时无极值点,在
时无极值点,在![]() 时,求出
时,求出![]() 的两根,可列表得出
的两根,可列表得出![]() 的正负,得
的正负,得![]() 的单调性,从而得极值点.
的单调性,从而得极值点.
(3)由(2)知![]() ,
,![]() ,求出
,求出![]() ,注意
,注意![]() 代换后可转化为
代换后可转化为![]() 的代数式,令
的代数式,令![]() ,首先有
,首先有![]() ,
,![]() 变为
变为![]() 的函数,由
的函数,由![]() 求出
求出![]() 的取值范围后可得
的取值范围后可得![]() 的取值范围.
的取值范围.
解:(1)定义域为![]() ,由题意得
,由题意得![]()
因为函数![]() 在定义域上是单调增函数,所以
在定义域上是单调增函数,所以![]() 在
在![]() 上恒成立
上恒成立
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上恒成立
上恒成立
因为![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以![]() ,即
,即![]() ,所以,实数a的取值范围为
,所以,实数a的取值范围为![]()
(2)![]() ,
,
①![]() 时,由第(1)问可知,函数
时,由第(1)问可知,函数![]() 在定义域上是单调增函数;
在定义域上是单调增函数;
所以![]() 无极值点,即
无极值点,即![]() 的极值点的个数为0
的极值点的个数为0
②![]() 时,令
时,令![]() ,得:
,得:![]() ,
,![]()
当![]() 时,
时,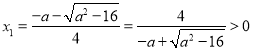 ,故
,故![]()
列表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| 极大值 |
| 极小值 |
|
当![]() 时,
时,![]() 有极大值,当
有极大值,当![]() 时,
时,![]() 有极小值
有极小值
所以,![]() 的极值点的个数为2
的极值点的个数为2
综上所述,当![]() 时,
时,![]() 的极值点的个数为0;当
的极值点的个数为0;当![]() 时,
时,![]() 的极值点的个数为2
的极值点的个数为2
(3)由题意知,![]() ,
,
因为![]() 是函数
是函数![]() 的两个极值点,所以是方程
的两个极值点,所以是方程![]() 的两个不等实根
的两个不等实根
所以![]() ,
,![]()
所以![]()
![]()
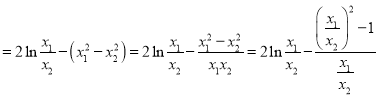
令![]() ,记
,记![]()
由![]() 可得:
可得:![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以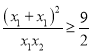 ,所以
,所以![]() ,即
,即![]() ,
,
因为![]() ,解得:
,解得:![]()
又![]() ,所以
,所以![]() 在
在![]() 上单调减
上单调减
所以![]()
所以![]() 的最小值为
的最小值为![]()


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
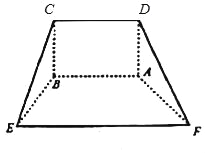
【题目】如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且![]() ,平面ABCD⊥平面ABEF
,平面ABCD⊥平面ABEF
(1)求证:BE⊥DF;
(2)求三棱锥C﹣AEF的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图象如图所示,点A,B,C在图象
的部分图象如图所示,点A,B,C在图象![]() 上,
上,![]() ,
,![]() ,并且
,并且![]() 轴
轴
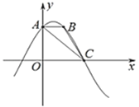
(1)求![]() 和
和![]() 的值及点B的坐标;
的值及点B的坐标;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)将函数![]() 的图象上各点的纵坐标变为原来的
的图象上各点的纵坐标变为原来的![]() 倍,横坐标不变,再将所得图象各点的横坐标变为原来的
倍,横坐标不变,再将所得图象各点的横坐标变为原来的![]() 倍,纵坐标不变,最后将所得图象向右平移
倍,纵坐标不变,最后将所得图象向右平移![]() 个单位,得到
个单位,得到![]() 的图象,若关于x的方程
的图象,若关于x的方程![]() 在区间
在区间![]() 上有两个不同解,求实数a的取值范围.
上有两个不同解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,底面为菱形的直四棱柱![]() 被过三点
被过三点![]() 的平面截去一个三棱锥
的平面截去一个三棱锥![]() (图一)得几何体
(图一)得几何体![]() (图二),E为
(图二),E为![]() 的中点.
的中点.
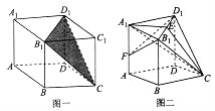
(1)点F为棱![]() 上的动点,试问平面
上的动点,试问平面![]() 与平面
与平面![]() 是否垂直?请说明理由;
是否垂直?请说明理由;
(2)设![]() ,当点F为
,当点F为![]() 中点时,求锐二面角
中点时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了激励业务员的积极性,对业绩在60万到200万的业务员进行奖励奖励方案遵循以下原则:奖金y(单位:万元)随着业绩值x(单位:万元)的增加而增加,且奖金不低于1.5万元同时奖金不超过业绩值的5%.
(1)若某业务员的业绩为100万核定可得4万元奖金,若该公司用函数![]() (k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知
(k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知![]() ,
,![]() )
)
(2)若采用函数![]() 作为奖励函数模型试确定最小的正整数a的值.
作为奖励函数模型试确定最小的正整数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:
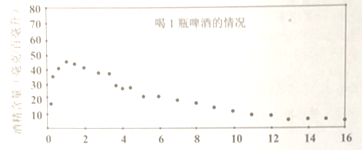
该函数模型如下:
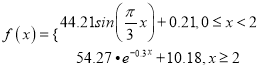
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国中医学的发展,药用昆虫的使用相应愈来愈多.每年春暖以后至寒冬前,是昆虫大量活动与繁殖季节,易于采集各种药用昆虫.已知一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
温度 | 10 | 11 | 13 | 12 | 8 |
产卵数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记这两天药用昆虫的产卵分别为![]() ,
,![]() ,求事件“
,求事件“![]() ,
,![]() 均不小于25”的概率;
均不小于25”的概率;
(2)科研人员确定的研究方案是:先从这五组数据中任选2组,用剩下的3组数据建立![]() 关于
关于![]() 的线性回归方程,再对被选取的2组数据进行检验.
的线性回归方程,再对被选取的2组数据进行检验.
(ⅰ)若选取的是3月2日与30日的两组数据,请根据3月7日、15日和22日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(ⅱ)若由线性回归方程得到的估计数据与选出的检验数据的误差均不超过2个,则认为得到的线性回归方程是可靠的,试问(ⅰ)中所得的线性回归方程是否可靠?
附:回归直线的斜率和截距的最小二乘估计公式分别为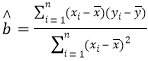 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com