
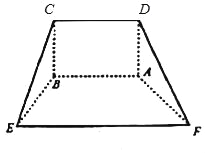
【题目】如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且![]() ,平面ABCD⊥平面ABEF
,平面ABCD⊥平面ABEF
(1)求证:BE⊥DF;
(2)求三棱锥C﹣AEF的体积V.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,利用勾股定理可得
,利用勾股定理可得![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]()
![]() 平面
平面![]() ,可得
,可得![]() ,由此可得
,由此可得![]()
![]() 平面
平面![]() ,则
,则![]()
![]() 平面
平面![]() ,从而可得结果;(2)
,从而可得结果;(2)![]() 平面
平面![]() ,可得
,可得![]() ,由(1)得,
,由(1)得,![]()
![]() 平面
平面![]() ,由棱锥的体积公式可得结果.
,由棱锥的体积公式可得结果.

(1)取EF的中点G,连结AG,
∵EF=2AB,∴AB=EG,
又AB∥EG,∴四边形ABEG为平行四边形,
∴AG∥BE,且AG=BE=AF=2,
在△AGF中,GF=![]() ,AG=AF=2,
,AG=AF=2,
∴![]() ,∴AG⊥AF,
,∴AG⊥AF,
∵四边形ABCD是矩形,∴AD⊥AB,
又平面ABCD⊥平面ABEF,且平面ABCD![]() 平面ABEF=AB,
平面ABEF=AB,
∴AD⊥平面ABEF,又AG![]() 平面ABEF,
平面ABEF,
∴AD⊥AG,
∵AD![]() AF=A,∴AG⊥平面ADF,
AF=A,∴AG⊥平面ADF,
∵AG∥BE,∴BE⊥平面ADF,
∵DF![]() 平面ADF,∴BE⊥DF;
平面ADF,∴BE⊥DF;
(2)∵CD∥AB且![]() 平面ABEF,BA
平面ABEF,BA![]() 平面ABEF,
平面ABEF,
∴CD∥平面ABEF,∴![]() ,
,
由(1)得,DA⊥平面ABEF,
∵![]() ,∴
,∴![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】据国家统计局发布的数据,2019年11月全国![]() (居民消费价格指数),同比上涨
(居民消费价格指数),同比上涨![]() ,
,![]() 上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响
上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响![]() 上涨3.27个百分点.下图是2019年11月
上涨3.27个百分点.下图是2019年11月![]() 一篮子商品权重,根据该图,下列四个结论正确的有______.
一篮子商品权重,根据该图,下列四个结论正确的有______.
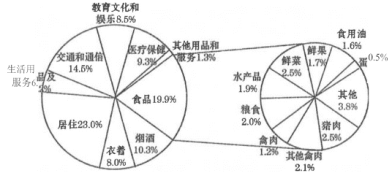
①![]() 一篮子商品中权重最大的是居住
一篮子商品中权重最大的是居住
②![]() 一篮子商品中吃穿住所占权重超过
一篮子商品中吃穿住所占权重超过![]()
③猪肉在![]() 一篮子商品中权重为
一篮子商品中权重为![]()
④猪肉与其他禽肉在![]() 一篮子商品中权重约为
一篮子商品中权重约为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,P,Q分别是线段
的棱长为1,P,Q分别是线段![]() 和
和![]() 上的动点,且满足
上的动点,且满足![]() ,则下列命题错误的是( )
,则下列命题错误的是( )

A.存在P,Q的某一位置,使![]()
B.![]() 的面积为定值
的面积为定值
C.当![]() 时,直线
时,直线![]() 与
与![]() 是异面直线
是异面直线
D.无论P,Q运动到任何位置,均有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法正确的是________.
,下列说法正确的是________.
①![]() 是
是![]() 的最大值点.
的最大值点.
②函数![]() 有且只有1个零点.
有且只有1个零点.
③存在正实数![]() ,使得
,使得![]() 恒成立.
恒成立.
④对任意两个不相等的正实数![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的数学家刘徽著有《海岛算经》.内有一篇:“今有望海岛,立两表齐、高三丈,前后相去千步,今后表与前表相直,从前表却行百二十三步,人目著地望岛峰,与表末参合.从后表却行百二十七步,人目著地取望岛峰,亦与表末参合.问岛高及去表各几何?”(参考译文:假设测量海岛,立两根标杆,高均为5步,前后相距1000步,令前后两根标杆的底部和岛的底部在同一水平直线上,从前标杆退行123步,人的视线从地面(人的高度忽略不计)过标杆顶恰好观测到岛峰,从后标杆退行127步,人的视线从地面过标杆顶恰好观测到岛峰,问岛高多少?岛与前标杆相距多远?)(丈、步为古时计量单位,三丈=5步).则海岛高度为
A. 1055步 B. 1255步 C. 1550步 D. 2255步
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com