
已知函数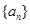 是首项为2,公比为
是首项为2,公比为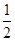 的等比数列,数列
的等比数列,数列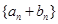 是首项为-2,第三项为2的等差数列.
是首项为-2,第三项为2的等差数列.
(1)求数列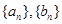 的通项式.
的通项式.
(2)求数列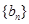 的前
的前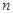 项和
项和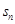 .
.
(1)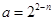 ,bn=2n-4-
,bn=2n-4-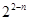 ; (2)Tn=n2-3n-4+
; (2)Tn=n2-3n-4+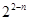 .
.
解析试题分析:(1)直接用等比数列等差数列即可求得数列{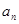 }{bn}的通项公式.
}{bn}的通项公式.
(2)数列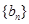 是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.
是一个等差数列与一个等比数列的和,故其求和采用分组求和的方法.
试题解析:(1)∵数列{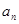 }是首项
}是首项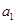 =2,公比q=
=2,公比q=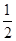 的等比数列,
的等比数列,
∴an=2·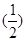 n-1=22-n,
n-1=22-n,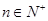 3分
3分
依题意得数列{bn+an}的公差d=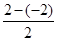 =2,
=2,
∴bn+an=-2+2(n-1)=2n-4,
∴bn=2n-4-22-n,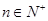 6分
6分
(2)设Sn为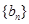 的前n项和,由(1)得 Sn=
的前n项和,由(1)得 Sn=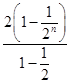 =4
=4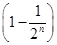 9分
9分
设数列{bn+an}的前n项和为Pn 则 Pn=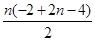 =n(n-3),
=n(n-3),
∴Tn=Pn-Sn=n(n-3)-4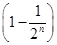 =n2-3n-4+22-n 12分
=n2-3n-4+22-n 12分
考点:等差数列等比数列的通项公式及前n项和公式


科目:高中数学 来源: 题型:解答题
已知正项数列{an}中,a1=1,且log3an,log3an+1是方程x2 (2n
(2n 1)x+bn=0的两个实根.
1)x+bn=0的两个实根.
(1)求a2,b1;
(2)求数列{an}的通项公式;
(3)若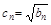 ,
,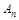 是
是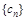 前
前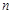 项和,
项和, 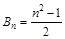 ,当
,当 时,试比较
时,试比较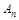 与
与 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列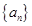 的各项都是正数,且对任意
的各项都是正数,且对任意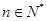 都有
都有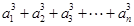
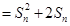 ,其中
,其中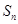 为数列
为数列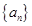 的前
的前 项和.
项和.
(1)求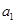 、
、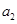 ;
;
(2)求数列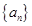 的通项公式;
的通项公式;
(3)设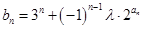 ,对任意的
,对任意的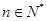 ,都有
,都有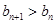 恒成立,求实数
恒成立,求实数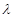 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知数列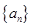 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为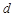 ,
, 为其前
为其前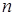 项和,且满足
项和,且满足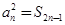 ,
,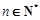 .数列
.数列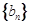 满足
满足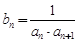 ,
,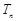 为数列
为数列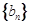 的前
的前 项和.
项和.
(1)求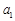 、
、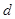 和
和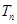 ;
;
(2)若对任意的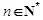 ,不等式
,不等式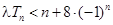 恒成立,求实数
恒成立,求实数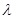 的取值范围;
的取值范围;
(3)是否存在正整数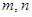
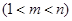 ,使得
,使得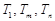 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有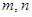 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在数列 中,如果存在非零的常数
中,如果存在非零的常数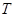 ,使
,使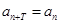 对于任意正整数
对于任意正整数 均成立,就称数列
均成立,就称数列 为周期数列,其中
为周期数列,其中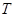 叫做数列
叫做数列 的周期. 已知数列
的周期. 已知数列 满足
满足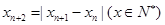 ,若
,若 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和为
的前2012项的和为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com