
关于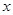 的方程
的方程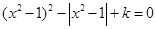 ,给出下列四个命题:
,给出下列四个命题:
①存在实数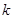 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数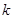 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数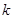 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数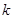 ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是
A.0 B.1 C.2 D.3
A
【解析】本题考查了分段函数,以及函数与方程的思想,数形结合的思想.还有作图能力。
关于x的方程(x2-1)2-|x2-1|+k=0可化为(x2-1)2-(x2-1)+k=0(x≥1或x≤-1)(1)或(x2-1)2+(x2-1)+k=0(-1<x<1)(2),当k=-2时,通过解一元二次方程可知,方程(1)的解为±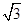 ,方程(2)无解,原方程恰有2个不同的实根
,方程(2)无解,原方程恰有2个不同的实根
当k=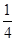 时,解一元二次方程可知,方程(1)有两个不同的实根±
时,解一元二次方程可知,方程(1)有两个不同的实根±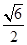 ,方程(2)有两个不同的实根±
,方程(2)有两个不同的实根±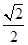 ,即原方程恰有4个不同的实根,
,即原方程恰有4个不同的实根,
当k=0时,解一元二次方程可知方程(1)的解为-1,+1,±
,方程(2)的解为x=0,原方程恰有5个不同的实根
当k=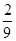 时,解一元二次方程可知方程(1)的解为±
时,解一元二次方程可知方程(1)的解为±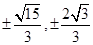 ,方程(2)的解为±
,方程(2)的解为±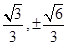 ,即原方程恰有8个不同的实根,故选A
,即原方程恰有8个不同的实根,故选A
解决该试题关键是将x的方程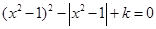 可化为(x2-1)2-|x2-1|=-k,画出函数y=(x2-1)2-|x2-1|和y=-k的图象可得解。
可化为(x2-1)2-|x2-1|=-k,画出函数y=(x2-1)2-|x2-1|和y=-k的图象可得解。


科目:高中数学 来源: 题型:
(06年湖北卷)关于![]() 的方程
的方程![]() ,给出下列四个命题: ( )
,给出下列四个命题: ( )
①存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数![]() ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
关于![]() 的方程
的方程![]() ,给出下列四个命题:
,给出下列四个命题:
①存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数![]() ,使得方程恰有8个不同的实根.
,使得方程恰有8个不同的实根.
其中假命题的个数是 ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省高三第三次模拟考试文科数学试卷(解析版) 题型:选择题
关于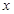 的方程
的方程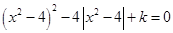 ,给出下列四个命题:
,给出下列四个命题:
①存在实数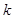 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数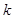 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数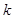 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数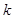 ,使得方程恰有8个不同的实根.
,使得方程恰有8个不同的实根.
其中假命题的个数是
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三上学期期中考试理科数学 题型:选择题
关于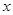 的方程
的方程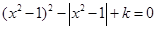 ,给出下列四个命题:
,给出下列四个命题:
①存在实数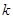 ,使得方程恰有2个不同实根;
,使得方程恰有2个不同实根;
②存在实数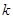 ,使得方程恰有4个不同实根;
,使得方程恰有4个不同实根;
③存在实数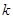 ,使得方程恰有5个不同实根;
,使得方程恰有5个不同实根;
④存在实数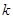 ,使得方程恰有8个不同实根;
,使得方程恰有8个不同实根;
其中假命题的个数是 ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com