
����Ŀ�����ڵ�ǰѧ����ҵ�������أ���������������ձ��½����ִ�ij���������ȡ16��ѧ������Уҽ�ö������������õ�ÿ��ѧ��������״���ľ�Ҷͼ����С����ǰ��һλ����Ϊ����С������һλ����ΪҶ����ͼ�� 
����ָ���������ݵ���������λ����
�������������Խ�����Ͷ�5.0�����Ϊ��������������Уҽ����16�������ѡȡ3�ˣ�������1���ǡ����������ĸ��ʣ�
��������16�˵�������������������ѧУ���������ݣ����Ӹ�У�������ࣩܶ��ѡ3�ˣ��Ǧα�ʾ�鵽����������ѧ������������εķֲ��м���ѧ������
���𰸡��⣺����4.6��4.7���������Σ�
��������4.6��4.7�������4.75
����������֪������һ���ŵ���ͣ�
��Ai��ʾ��ȡ3������i�����ǡ�����������
������1���ǡ�����������Ϊ�¼�A��������һ�����Ǻ���������������Ǻ�������
�� ![]() ��
��
���εĿ���ȡֵΪ0��1��2��3
![]() ��ֲ���Ϊ
��ֲ���Ϊ
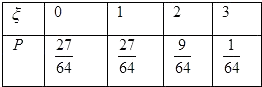
��E��=1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() =0.75
=0.75
����������1�����������ľ�Ҷͼ����16�����ݣ��ҳ���������λ������λ����Ҫ���մ�С�����˳�����еõ����ۣ���2��������֪������һ���ŵ���ͣ�������1���ǡ���������������һ�����Ǻ���������������Ǻ����������ݹŵ����ʽ�õ��������3�����ڴӸ�У��ѡ3�ˣ��Ǧα�ʾ�鵽����������ѧ�����������õ������Ŀ���ȡֵ��0��1��2��3����ϱ�����Ӧ���¼���������ʣ�д���ֲ��к�������
�����㾫����������Ŀ����֪���������þ�Ҷͼ��ƽ��������λ�������������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���վ�Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ��٣���ƽ��������������λ����������һ�����ݼ������Ƶ�������ƽ��������������λ�����е�λ����ƽ������ӳһ�����ݵ�ƽ��ˮƽ�������������е�ÿ�������й�ϵ��������Ϊ��Ҫ��Ӧ����㣻����λ�����ܸ���ƫ���ƫС���ݵ�Ӱ�죻��������������ݳ��ֵ�Ƶ���йأ����ܸ������ݵ�Ӱ�죬��ʱ��������Ϊ���ĵ����ݣ�


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD��A1B1C1D1�У�E��F�ֱ�Ϊ��BB1��BC���е㣬������ֱ��AB1��EF���ɽǵĴ�СΪ�� ��
A.30��
B.45��
C.60��
D.90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����P��ABC�ĵ����ǵ���ֱ�������Σ��ҡ�ACB= ![]() ������PAB�͵���ABC��AB=PA=PB=2�����������������ͼ�б�ע�ijߴ�x��y��z�ֱ��ǣ� ��
������PAB�͵���ABC��AB=PA=PB=2�����������������ͼ�б�ע�ijߴ�x��y��z�ֱ��ǣ� �� 
A.![]() ��1��
��1�� ![]()
B.![]() ��1��1
��1��1
C.2��1�� ![]()
D.2��1��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ADEF������ABCD����ƽ�滥�ഹֱ����ͼ������AF=1��AD=2����ADC= ![]() ����Nʱ�߶�AD���е㣮
����Nʱ�߶�AD���е㣮 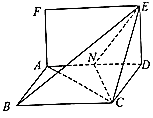
�����������߶�BE���Ƿ���ڵ�M��ʹ��ֱ��AF��ƽ��MNC�������ڣ���֤��AF��ƽ��MNC������� ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
����������N��CE��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC����x�� ![]() ��2+��y��1��2=1������A����t��0����B��t��0����t��0������ԲC�ϴ��ڵ�P��ʹ�á�APB=90�㣬��tȡ�����ֵʱ����P�������ǣ� ��
��2+��y��1��2=1������A����t��0����B��t��0����t��0������ԲC�ϴ��ڵ�P��ʹ�á�APB=90�㣬��tȡ�����ֵʱ����P�������ǣ� ��
A.�� ![]() ��
�� ![]() ��
��
B.�� ![]() ��
�� ![]() ��
��
C.�� ![]() ��
�� ![]() ��
��
D.�� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x�� ![]() |+|x+m|����m��0��
|+|x+m|����m��0��
��I��֤����f��x����4
��II����f��1����5����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x��1��ex+ ![]() ������a��R����������㣬��a��ȡֵ��Χ�� ��
������a��R����������㣬��a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=sin����x+�գ�+cos����x+�գ����أ�0��|��|�� ![]() ������С������Ϊ�У���f����x��=f��x������ ��
������С������Ϊ�У���f����x��=f��x������ ��
A.f��x���ڣ�0�� ![]() ����������
����������
B.f��x���ڣ� ![]() ��
�� ![]() �������ݼ�
�������ݼ�
C.f��x���ڣ� ![]() ��
�� ![]() ����������
����������
D.f��x���ڣ� ![]() ���У���������
������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2013����2016���ڼ䣬��ÿ��6��1�ն������д���mԪ��һ�궨�ڴ����������Ϊq���ֲ��䣬��ÿ�굽�ڵĴ�Ϣ�Զ�תΪ�µ�һ�궨�ڣ���2017��6��1�ռ�ȥ���в��ٴ����ǽ����д��ı�Ϣȫ��ȡ�أ���ȡ�صĽ���ǣ� ��
A.m��1+q��4Ԫ
B.m��1+q��5Ԫ
C.![]() Ԫ
Ԫ
D.![]() Ԫ
Ԫ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com