
【题目】已知函数f(x)=(x﹣1)ex+ ![]() (其中a∈R)有两个零点,则a的取值范围是 .
(其中a∈R)有两个零点,则a的取值范围是 .
【答案】(﹣∞,﹣1)∪(﹣1,0)
【解析】解:f′(x)=)=(x﹣1)ex+ex+ax=x(ex+a),
①当a≥0时,ex+a>0,∴x∈(﹣∞,0)时,f′(x)<0,x∈(0,+∞)时,f′(x)>0,
f(x)在(﹣∞,0)递减,在(0,+∞)递增,且f(0)=0,
此时f(x)=(x﹣1)ex+ ![]() (其中a∈R)不存在有两个零点;
(其中a∈R)不存在有两个零点;
②当a=﹣1时,f′(x)≥0恒成立,函数f(x)单调,此时f(x)=(x﹣1)ex+ ![]() (其中a∈R)不存在有两个零点;
(其中a∈R)不存在有两个零点;
③当a<0且a≠﹣1时,令f′(x)=0,解得x1=0,x2=ln(﹣a) (a≠﹣1).
a∈(﹣1,0)时,x2<0,函数在(﹣∞,ln(﹣a)))递增,在(ln(﹣a),0)递减,在(0,+∞)递增,而f(0)=0,此时函数恰有两个零点;
a∈(﹣∞,﹣1),时,x2>0,函数在(﹣∞,0)递增,在(0,ln(﹣a))递减,在(ln(﹣a),+∞)递增,而f(0)=0,此时函数恰有两个零点;
综上,则a的取值范围是:(﹣∞,﹣1)∪(﹣1,0)
所以答案是:(﹣∞,﹣1)∪(﹣1,0)


科目:高中数学 来源: 题型:
【题目】定义max{a,b}= ![]() ,已知函数f(x)=max{|2x﹣1|,ax2+b},其中a<0,b∈R,若f(0)=b,则实数b的范围为 , 若f(x)的最小值为1,则a+b= .
,已知函数f(x)=max{|2x﹣1|,ax2+b},其中a<0,b∈R,若f(0)=b,则实数b的范围为 , 若f(x)的最小值为1,则a+b= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,PA、PB、PC互相垂直,PA=PB=1,M是线段BC上一动点,若直线AM与平面PBC所成角的正切的最大值是 ![]() ,则三棱锥P﹣ABC的外接球的表面积是( )
,则三棱锥P﹣ABC的外接球的表面积是( )
A.2π
B.4π
C.8π
D.16π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图: 
(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( ) 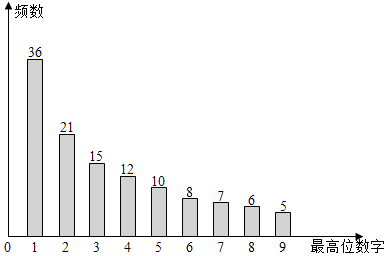
A.P=lg(1+ ![]() )
)
B.P= ![]()
C.P= ![]()
D.P= ![]() ×
× ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+b(a,b∈R),曲线f(x)在x=1处的切线方程为x﹣y﹣1=0.
(Ⅰ)求a,b的值;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)已知满足xlnx=1的常数为k.令函数g(x)=mex+f(x)(其中e是自然对数的底数,e=2.71828…),若x=x0是g(x)的极值点,且g(x)≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R,函数 ![]() ,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
(Ⅰ)求b的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若g(x)>f(x)在区间(﹣∞,0)内恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x,y∈R,且 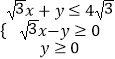 ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 点(n,Sn+3)(n∈N*)在函数y=3×2x的图象上,等比数列{bn}满足bn+bn+1=an(n∈N*).其前n项和为Tn , 则下列结论正确的是( )
A.Sn=2Tn
B.Tn=2bn+1
C.Tn>an
D.Tn<bn+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com