
【题目】利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( ) 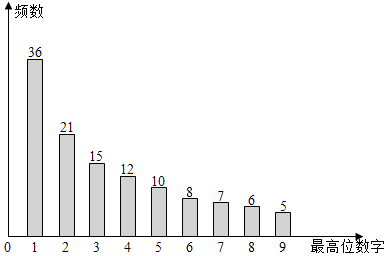
A.P=lg(1+ ![]() )
)
B.P= ![]()
C.P= ![]()
D.P= ![]() ×
× ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax(a∈R).
(1)若曲线y=f(x)存在一条切线与直线y=x平行,求a的取值范围;
(2)当0<a<2时,若f(x)在[a,2]上的最大值为﹣ ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣lnx(ln2≈﹣0.693, ![]() ≈1.648,均为不足近似值)
≈1.648,均为不足近似值)
(1)当x≥1时,判断函数f(x)的单调性;
(2)证明:当x>0时,不等式f(x)> ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣ ![]() )2+(y﹣1)2=1和两点A(﹣t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )
)2+(y﹣1)2=1和两点A(﹣t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)经过点(1,
=1(a>b>0)经过点(1, ![]() ),离心率为
),离心率为 ![]() ,点A为椭圆C的右顶点,直线l与椭圆相交于不同于点A的两个点P(x1 , y1),Q(x2 , y2).
,点A为椭圆C的右顶点,直线l与椭圆相交于不同于点A的两个点P(x1 , y1),Q(x2 , y2).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)当 ![]() ⊥
⊥ ![]() =0时,求△OPQ面积的最大值.
=0时,求△OPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() |﹣
|﹣ ![]() |,其中﹣3≤a≤1.
|,其中﹣3≤a≤1.
(Ⅰ)当a=1时,解不等式f(x)≥1;
(Ⅱ)对于任意α∈[﹣3,1],不等式f(x)≥m的解集为空集,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 
(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)若二面角P﹣CD﹣B为45°,AD=2,CD=3,求点F到平面PCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知C1: ![]() (θ为参数),将C1上的所有点的横坐标、纵坐标分别伸长为原来的
(θ为参数),将C1上的所有点的横坐标、纵坐标分别伸长为原来的 ![]() 和2倍后得到曲线C2以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(
和2倍后得到曲线C2以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ( ![]() cosθ+sinθ)=4
cosθ+sinθ)=4
(1)试写出曲线C1的极坐标方程与曲线C2的参数方程;
(2)在曲线C2上求一点P,使点P到直线l的距离最小,并求此最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com