
【题目】已知函数f(x)=xex﹣lnx(ln2≈﹣0.693, ![]() ≈1.648,均为不足近似值)
≈1.648,均为不足近似值)
(1)当x≥1时,判断函数f(x)的单调性;
(2)证明:当x>0时,不等式f(x)> ![]() 恒成立.
恒成立.
【答案】
(1)解:对f(x)=xex﹣lnx求导得f′(x)=(x+1)ex﹣ ![]() ,
,
∵x≥1时,(x+1)ex≥2e, ![]() ≤1,
≤1,
∴f′(x)≥2e﹣1>0,
∴f(x)在[1,+∞)递增
(2)证明:∵f′( ![]() )=1.25
)=1.25 ![]() ﹣4<1.25×2﹣4<0,
﹣4<1.25×2﹣4<0,
f′( ![]() )=
)= ![]() ﹣2>
﹣2> ![]() ×1.648﹣2=0.472>0,
×1.648﹣2=0.472>0,
又f′(x)在(0,+∞)递增,
∴f′(x)在(0,+∞)内有唯一1个零点x0,
且(x0+1) ![]() =
= ![]() ,x0∈(
,x0∈( ![]() ,
, ![]() ),
),
∴x=x0是f(x)在(0,+∞)上唯一的极小值点,也是最小值值点,
∴f(x)≥f(x0)=x0![]() ﹣lnx0=
﹣lnx0= ![]() ﹣lnx0,
﹣lnx0, ![]() <x0<
<x0< ![]() ,
,
∴f(x)在[ ![]() ,
, ![]() ]递减,
]递减,
∴f(x0)≥f( ![]() )=
)= ![]() +ln2>
+ln2> ![]() +0.639>1.359>
+0.639>1.359> ![]() ,
,
∴f(x)> ![]()
【解析】(1)求出函数的导数,判断导函数的符合,求出函数的单调区间即可;(2)求出函数的导数,根据函数的单调性证明即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=4,an+1= ![]() ,n∈N* , Sn为{an}的前n项和.
,n∈N* , Sn为{an}的前n项和.
(Ⅰ)求证:n∈N*时,an>an+1;
(Ⅱ)求证:n∈N*时,2≤Sn﹣2n< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1= ![]() ,Sn=n2an﹣n(n﹣1),n=1,2,…
,Sn=n2an﹣n(n﹣1),n=1,2,…
(1)证明:数列{ ![]() Sn}是等差数列,并求Sn;
Sn}是等差数列,并求Sn;
(2)设bn= ![]() ,求证:b1+b2+…+bn<
,求证:b1+b2+…+bn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,PA、PB、PC互相垂直,PA=PB=1,M是线段BC上一动点,若直线AM与平面PBC所成角的正切的最大值是 ![]() ,则三棱锥P﹣ABC的外接球的表面积是( )
,则三棱锥P﹣ABC的外接球的表面积是( )
A.2π
B.4π
C.8π
D.16π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数p(x)=lnx+x﹣4,q(x)=axex(a∈R).
(Ⅰ)若a=e,设f(x)=p(x)﹣q(x),试证明f′(x)存在唯一零点x0∈(0, ![]() ),并求f(x)的最大值;
),并求f(x)的最大值;
(Ⅱ)若关于x的不等式|p(x)|>q(x)的解集中有且只有两个整数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( ) 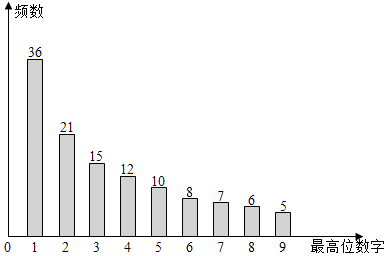
A.P=lg(1+ ![]() )
)
B.P= ![]()
C.P= ![]()
D.P= ![]() ×
× ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com