
【题目】已知函数f(x)=lnx﹣ax(a∈R).
(1)若曲线y=f(x)存在一条切线与直线y=x平行,求a的取值范围;
(2)当0<a<2时,若f(x)在[a,2]上的最大值为﹣ ![]() ,求a的值.
,求a的值.
【答案】
(1)f′(x)= ![]() ﹣a,
﹣a,
若曲线y=f(x)存在一条切线与直线y=x平行,
则 ![]() ﹣a=1,即a=
﹣a=1,即a= ![]() ﹣1有解,
﹣1有解,
由x>0,得:a>﹣1
(2)f′(x)= ![]() ﹣a,
﹣a,
令f′(x)>0,解得:0<x< ![]() ,
,
令f′(x)<0,解得:x> ![]() ,
,
故f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,+∞)递减,
,+∞)递减,
①2≤ ![]() 即0<a≤
即0<a≤ ![]() 时,
时,
f(x)在[a,2]递增,f(x)max=f(2)=ln2﹣2a=﹣ ![]() ,
,
解得:a= ![]() ln2+
ln2+ ![]() >
> ![]() (舍);
(舍);
②a< ![]() <2即
<2即 ![]() <a<1时,
<a<1时,
f(x)在[a, ![]() )递增,在(
)递增,在( ![]() ,2]递减,
,2]递减,
故f(x)max=f( ![]() )=ln
)=ln ![]() ﹣1=﹣
﹣1=﹣ ![]() ,
,
解得:a= ![]() ,
,
③ ![]() ≤a,即1≤a<2时,
≤a,即1≤a<2时,
f(x)在[a,2]递减,f(x)max=f(a)=lna﹣a2=﹣ ![]() ,
,
函数n(a)=lna﹣a2,a∈[1,2),n′(a)= ![]() ﹣2a递减,n′(1)=﹣1<0,
﹣2a递减,n′(1)=﹣1<0,
故n(a)在[1,2)递减,n(a)<n(1)=﹣1<﹣ ![]() ,
,
故方程lna﹣a2=﹣ ![]() 无解;
无解;
综上a= ![]()
【解析】(1)求出函数的导数,得到关于a的函数式,根据函数的单调性求出a的范围即可;(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的最大值,得到关于a的方程,解出即可.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点,F1(﹣c,0),F2(c,0),P为C1与C2在第一象限的交点,|PF1|=|F1F2|且|PF2|=5,若椭圆C1的离心率 ![]() ,则双曲线的离心率e2的范围是( )
,则双曲线的离心率e2的范围是( )
A.![]()
B.![]()
C.(2,3)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB= ![]() ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点. 
(Ⅰ)求证:CE∥平面PAF;
(Ⅱ)在线段BC上是否存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°?若存在,试确定G的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代一部重要的数学著作,书中有如下问题:“今有良马与驽马发长安,至齐.齐去长安三千里,良马初日行一百九十三里,日增一十三里,驾马初日行九十七里,日减半里.良马先至齐,复还迎驽马.何日相逢,”其大意为:“现在有良马和驽马同时从长安出发到齐去,已知长安和齐的距离是3000里,良马第一天行193里,之后每天比前一天多行13里,驽马第一天行97里,之后每天比前一天少行0.5里.良马到齐后,立刻返回去迎驽马,多少天后两马相遇.”现有三种说法:①驽马第九日走了93里路;②良马四日共走了930里路;③行驶5天后,良马和驽马相距615里. 那么,这3个说法里正确的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义max{a,b}= ![]() ,已知函数f(x)=max{|2x﹣1|,ax2+b},其中a<0,b∈R,若f(0)=b,则实数b的范围为 , 若f(x)的最小值为1,则a+b= .
,已知函数f(x)=max{|2x﹣1|,ax2+b},其中a<0,b∈R,若f(0)=b,则实数b的范围为 , 若f(x)的最小值为1,则a+b= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=4,an+1= ![]() ,n∈N* , Sn为{an}的前n项和.
,n∈N* , Sn为{an}的前n项和.
(Ⅰ)求证:n∈N*时,an>an+1;
(Ⅱ)求证:n∈N*时,2≤Sn﹣2n< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1= ![]() ,Sn=n2an﹣n(n﹣1),n=1,2,…
,Sn=n2an﹣n(n﹣1),n=1,2,…
(1)证明:数列{ ![]() Sn}是等差数列,并求Sn;
Sn}是等差数列,并求Sn;
(2)设bn= ![]() ,求证:b1+b2+…+bn<
,求证:b1+b2+…+bn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( ) 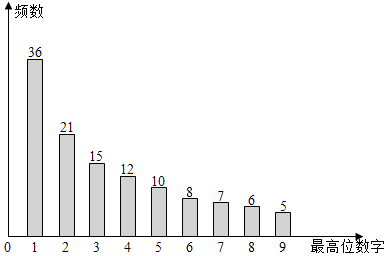
A.P=lg(1+ ![]() )
)
B.P= ![]()
C.P= ![]()
D.P= ![]() ×
× ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com