
【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点,F1(﹣c,0),F2(c,0),P为C1与C2在第一象限的交点,|PF1|=|F1F2|且|PF2|=5,若椭圆C1的离心率 ![]() ,则双曲线的离心率e2的范围是( )
,则双曲线的离心率e2的范围是( )
A.![]()
B.![]()
C.(2,3)
D.![]()
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如表: 
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则5288用算筹式可表示为 .
,则5288用算筹式可表示为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
(Ⅰ)求用含θ的代数式表示DC;
(Ⅱ)求△BCD面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在正常数a,b,使得x∈R有f(x+a)≤f(x)+b恒成立,则称f(x)为“限增函数”.给出下列三个函数:①f(x)=x2+x+1;② ![]() ;③f(x)=sin(x2),其中是“限增函数”的是( )
;③f(x)=sin(x2),其中是“限增函数”的是( )
A.①②③
B.②③
C.①③
D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且 ![]() .
.
(1)求抛物线的方程;
(2)如图所示,过F的直线l与抛物线相交于A,D两点,与圆x2+(y﹣1)2=1相交于B,C两点(A,B两点相邻),过A,D两点分别作我校的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为X,求X的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值(精确到0.01),并说明理由.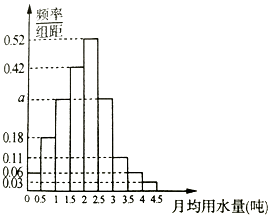
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行如图所示的程序框图,若输出的结果是8,则判断框内m的取值范围是( ) 
A.(30,42]
B.(42,56]
C.(56,72]
D.(30,72)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在圆C:x2+y2=4上,而Q为P在x轴上的投影,且点N满足 ![]() ,设动点N的轨迹为曲线E.
,设动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若A,B是曲线E上两点,且|AB|=2,O为坐标原点,求△AOB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax(a∈R).
(1)若曲线y=f(x)存在一条切线与直线y=x平行,求a的取值范围;
(2)当0<a<2时,若f(x)在[a,2]上的最大值为﹣ ![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com