
分析 根据题意,令x<0,则-x>0,结合函数[0,+∞)上的解析式可得f(-x)=-4x+3,又由函数为偶函数可得x<0时函数的解析式;进而综合2种情况可得答案.
解答 解:根据题意,令x<0,则-x>0,
则f(-x)=4(-x)+3=-4x+3,
又由f(x)为偶函数,则f(x)=f(-x)=-4x+3,
故f(x)=$\left\{\begin{array}{l}{4x+3,x≥0}\\{-4x+3,x<0}\end{array}\right.$,
故答案为:f(x)=$\left\{\begin{array}{l}{4x+3,x≥0}\\{-4x+3,x<0}\end{array}\right.$.
点评 本题考查函数的奇偶性的运用,涉及函数解析式的求法,注意将函数的解析式写成分段函数的形式.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:选择题
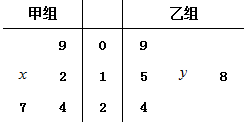 如图的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x、y的值分别为( )
如图的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x、y的值分别为( )| A. | 2,5 | B. | 5,5 | C. | 5,8 | D. | 8,8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | ±$\frac{1}{2}$ | D. | ±$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com