

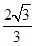 .
.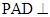 平面
平面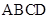 ,且
,且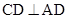 ,可证
,可证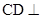 平面
平面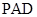 ,再根据
,再根据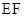 是中位线,可证
是中位线,可证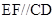 ,从而
,从而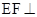 平面
平面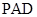 ,进而再证平面
,进而再证平面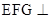 平面
平面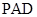 ,该题实质是先找到面
,该题实质是先找到面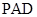 的一条垂线
的一条垂线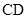 ,再将
,再将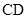 平移到面
平移到面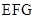 内;
内;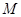 是线段
是线段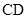 的动点,考虑到
的动点,考虑到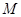 和
和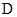 到面
到面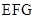 的距离相等,故
的距离相等,故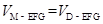 ,再结合第(1)问结果,取
,再结合第(1)问结果,取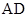 的中点
的中点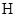 连接
连接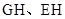 ,据面面垂直的性质,点
,据面面垂直的性质,点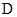 到
到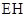 的距离就是三棱锥
的距离就是三棱锥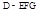 的高,再求
的高,再求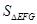 ,进而求体积.
,进而求体积.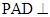 平面
平面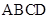 ,平面
,平面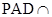 平面
平面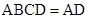 ,
,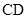
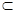 平面
平面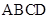 ,
,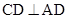 ,
,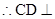 平面
平面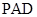 ,又
,又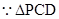 中,
中, 分别是
分别是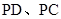 的中点,
的中点, ,可得
,可得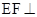 平面
平面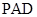 ,
,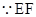
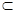 平面
平面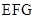 ,∴平面
,∴平面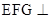 平面
平面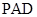 ;
;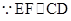 ,
,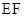
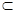 平面
平面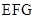 ,
,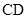
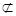 平面
平面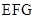 ,
,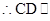 平面
平面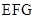 ,因此
,因此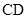 上的点
上的点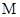 到平面
到平面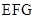 的距离等于点
的距离等于点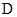 到平面
到平面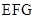 的距离,∴
的距离,∴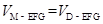 ,取
,取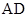 的中点
的中点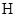 连接
连接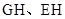 ,则
,则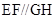 ,
,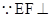 平面
平面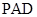 ,
,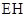
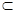 平面
平面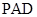 ,∴
,∴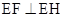 ,于是
,于是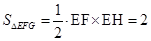 ,
,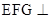 平面
平面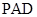 ,平面
,平面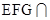 平面
平面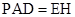 ,
,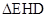 是正三角形,∴点
是正三角形,∴点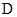 到平面
到平面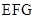 的距离等于正
的距离等于正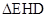 的高,即为
的高,即为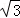 ,因此,三棱锥M﹣EFG的体积
,因此,三棱锥M﹣EFG的体积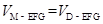 =
=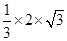 =
=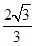 .
.

科目:高中数学 来源:不详 题型:解答题
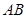 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.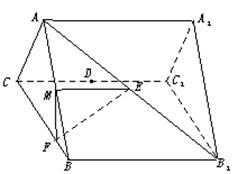
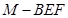 的体积.
的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
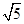 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
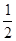 ,则其体积缩小到原来的
,则其体积缩小到原来的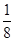 ;
;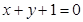 与圆
与圆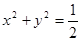 相切.
相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com