
【题目】已知函数f(x)在(-1,1)上有定义,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(![]() ),试证明
),试证明
(1)f(x)为奇函数;(2)f(x)在(-1,1)上单调递减
【答案】(1)见解析; (2)见解析.
【解析】
(1)令x=y=0可得f(0)=0,令y=-x,可得f(-x)=-f(x),故得证;(2)由单调性的定义,任取x1,x2∈(-1,1),且x1<x2,由性质可得可得f(x2)-f(x1)=f(x2)+f(-x1)=f(![]() ,由已知可判f(
,由已知可判f(![]() )<0,进而得证.
)<0,进而得证.
证明:(1)由f(x)+f(y)=f(![]() )可令x=y=0,得f(0)=0,
)可令x=y=0,得f(0)=0,
令y=-x,得f(x)+f(-x)=f(![]() )=f(0)=0 ∴f(x)=-f(-x) ∴f(x)为奇函数
)=f(0)=0 ∴f(x)=-f(-x) ∴f(x)为奇函数
(2)先证f(x)在(0,1)上单调递减
令0<x1<x2<1,则f(x2)-f(x1)=f(x2)+f(-x1)=f(![]() )
)
∵0<x1<x2<1,∴x2-x1>0,1-x1x2>0,∴![]() >0,
>0,
又(x2-x1)-(1-x2x1)=(x2-1)(x1+1)<0,∴x2-x1<1-x2x1,
∴0<![]() <1,由题意知f(
<1,由题意知f(![]() )<0, 即 f(x2)<f(x1)
)<0, 即 f(x2)<f(x1)
∴f(x)在(0,1)上为减函数,又f(x)为奇函数且f(0)=0
∴f(x)在(-1,1)上为减函数


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为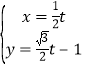 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 的线性回归直线方程为
的线性回归直线方程为![]() ,且
,且![]() ,
,![]() 之间的一组相关数据如下表所示,则下列说法错误的为
之间的一组相关数据如下表所示,则下列说法错误的为

A.变量![]() ,
,![]() 之间呈现正相关关系B.可以预测,当
之间呈现正相关关系B.可以预测,当![]() 时,
时,![]()
C.![]() D.由表格数据可知,该回归直线必过点
D.由表格数据可知,该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (a>0,且a≠1)的反函数为
(a>0,且a≠1)的反函数为![]() ,函数y=g(x)的图像与
,函数y=g(x)的图像与![]() 的图像关于点(a,0)对称。
的图像关于点(a,0)对称。
(1)求函数y=g(x)的解析式。
(2)是否存在实数a,使得当![]() 时,恒有
时,恒有![]() 成立?若存在,求出a的取值范围;若不存在,说明理由。
成立?若存在,求出a的取值范围;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如城镇小汽车的普及率为75%,即平均每100个家庭有75个家庭拥有小汽车,若从如城镇中任意选出5个家庭,则下列结论成立的是( )
A.这5个家庭均有小汽车的概率为![]()
B.这5个家庭中,恰有三个家庭拥有小汽车的概率为![]()
C.这5个家庭平均有3.75个家庭拥有小汽车
D.这5个家庭中,四个家庭以上(含四个家庭)拥有小汽车的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD="40" m,则电视塔的高度为多少?
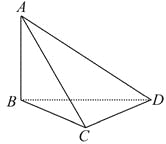
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com