
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①f(x)是周期函数;②f(x)的图象关于直线x=2kπ(k∈Z)对称,
③f(x)在(﹣π,0)上没有零点;④f(x)的值域为![]() ,
,
其中正确结论的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
计算f(x+2π)=f(x),①正确,f(x)是偶函数,即图象关于y轴对称,且周期为2π,②正确,计算f(![]() )=0,③错误,x∈[0,π]时,f(x)∈[
)=0,③错误,x∈[0,π]时,f(x)∈[![]() ,2],④正确,得到答案.
,2],④正确,得到答案.
对于①,因为f(x+2π)=|sin(x+2π)|![]() cos(x+2π)=|sinx|+cosx=f(x),所以f(x)是周期函数,故①正确;
cos(x+2π)=|sinx|+cosx=f(x),所以f(x)是周期函数,故①正确;
对于②,因为f(x)是偶函数,即图象关于y轴对称,且周期为2π,则图象关于直线2kπ(k∈Z)对称,故②正确;
对于③,因为f(![]() )=|sin(
)=|sin(![]() )|
)|![]() cos(
cos(![]() )
)![]() (
(![]() )=0,即x
)=0,即x![]() 时f(x)在(﹣π,0)上的零点,故③错误;
时f(x)在(﹣π,0)上的零点,故③错误;
对于④,函数f(x)是偶函数且周期为2π,则f(x)值域即为f(x)在[0,π]上的值域,
当x∈[0,π]时,f(x)=sinx![]() cosx=2sin(x
cosx=2sin(x![]() ),则x
),则x![]() ∈[
∈[![]() ,
,![]() ],
],
所以f(x)∈[![]() ,2],故④正确,
,2],故④正确,
故选:C.


科目:高中数学 来源: 题型:
【题目】已知定直线![]() ,定点
,定点![]() ,以坐标轴为对称轴的椭圆
,以坐标轴为对称轴的椭圆![]() 过点
过点![]() 且与
且与![]() 相切.
相切.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)椭圆的弦![]() 的中点分别为
的中点分别为![]() ,若
,若![]() 平行于
平行于![]() ,则
,则![]() 斜率之和是否为定值? 若是定值,请求出该定值;若不是定值请说明理由.
斜率之和是否为定值? 若是定值,请求出该定值;若不是定值请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.

(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ2(cos2θ+3sin2θ)=12,直线l的参数方程为![]() (t为参数),直线l与曲线C交于M,N两点.
(t为参数),直线l与曲线C交于M,N两点.
(1)若点P的极坐标为(2,π),求|PM||PN|的值;
(2)求曲线C的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆节假期期间,某商场为掌握假期期间顾客购买商品人次,统计了10月1日7:00﹣23:00这一时间段内顾客购买商品人次,统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的的频率分布直方图如下图所示,其中时间段7:0011:00,11:0015:00,15:00~19:00,19:00~23:00,依次记作[7,11),[11,15),[15,19),[19,23].
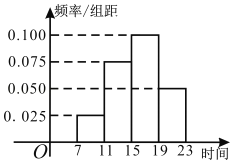
(1)求该天顾客购买商品时刻的中位数t与平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)由频率分布直方图可以近似认为国庆节假期期间该商场顾客购买商品时刻服从正态分布N(μ,δ2),其中μ近似为![]() ,δ=3.6,估计2019年国庆节假期期间(10月1日﹣10月7日)该商场顾客在12:12﹣19:24之间购买商品的总人次(结果保留整数);
,δ=3.6,估计2019年国庆节假期期间(10月1日﹣10月7日)该商场顾客在12:12﹣19:24之间购买商品的总人次(结果保留整数);
(3)为活跃节日气氛,该商场根据题中的4个时间段分组,采用分层抽样的方法从这5000个样本中随机抽取10个样本(假设这10个样本为10个不同顾客)作为幸运客户,再从这10个幸运客户中随机抽取4人每人奖励500元购物券,其他幸运客户每人奖励200元购物券,记获得500元购物券的4人中在15:00﹣19:00之间购买商品的人数为X,求X的分布列与数学期望;
参考数据:若T~N(μ,σ2),则①P(μ﹣σ<T≤μ+σ)=0.6827;②P(μ﹣2σ<T≤μ+2σ)=0.9545;③P(μ﹣3σ<T≤μ+3σ)=0.9973.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为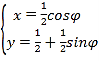 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() 、
、![]() (
(![]() 、
、![]() 异于原点),当斜率
异于原点),当斜率![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以![]() 为直径的圆,且
为直径的圆,且![]() 米,景观湖边界
米,景观湖边界![]() 与
与![]() 平行且它们间的距离为
平行且它们间的距离为![]() 米.开发商计划从
米.开发商计划从![]() 点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作
点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作![]() .设
.设![]() .
.
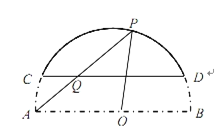
(1)用![]() 表示线段
表示线段![]() 并确定
并确定![]() 的范围;
的范围;
(2)为了使小区居民可以充分地欣赏湖景,所以要将![]() 的长度设计到最长,求
的长度设计到最长,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市春节大酬宾,购物满100元可参加一次抽奖活动,规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的人口处,小球在自由落下的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,顾客相应获得袋子里的奖品.已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
.若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com