
已知a,b,c∈{正实数},且a2+b2=c2,当n∈N,n>2时比较cn与an+bn的大小.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:解答题
设数列{an}满足a1=3,an+1=an2-2nan+2,n=1,2,3,…
(1)求a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);
(2)记Sn为数列{an}的前n项和,试求使得Sn<2n成立的最小正整数n,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:选择题
已知a>0,b>0,若不等式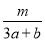 -
- -
- ≤0恒成立,则m的最大值为( )
≤0恒成立,则m的最大值为( )
A.4 B.16 C.9 D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:解答题
设二次函数f(x)=ax2+bx+c,函数F(x)=f(x)-x的两个零点为m,n(m<n).
(1)若m=-1,n=2,求不等式F(x)>0的解集;
(2)若a>0,且0<x<m<n<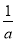 ,比较f(x)与m的大小.
,比较f(x)与m的大小.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:选择题
已知二次函数f(x)=ax2-(a+2)x+1(a∈Z),且函数f(x)在(-2,-1)上恰有一个零点,则不等式f(x)>1的解集为( )
A.(-∞,-1)∪(0,+∞) B.(-∞,0)∪(1,+∞)
C.(-1,0) D.(0,1)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:解答题
已知关于x的不等式(ax-5)(x2-a)<0的解集为M.
(1)当a=4时,求集合M;
(2)当3∈M,且5∉M时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:选择题
若α、β满足-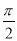 <α<β<
<α<β<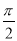 ,则α-β的取值范围是( )
,则α-β的取值范围是( )
A.-π<α-β<π B.-π<α-β<0
C.- <α-β<
<α-β<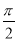 D.-
D.- <α-β<0
<α-β<0
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:填空题
设数列{an}中,若an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”,已知数列{bn}为“凸数列”,且b1=1,b2=-2,则数列{bn}的前2014项和为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-2等差数列及其前n项和(解析版) 题型:选择题
若等差数列的第一、二、三项依次是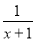 、
、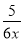 、
、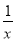 ,则数列的公差d是( )
,则数列的公差d是( )
A.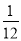 B.
B.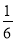 C.
C.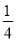 D.
D.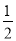
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com