
设数列{an}中,若an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”,已知数列{bn}为“凸数列”,且b1=1,b2=-2,则数列{bn}的前2014项和为________.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:解答题
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求 +
+ +
+ +…+
+…+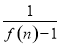 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:解答题
已知a,b,c∈{正实数},且a2+b2=c2,当n∈N,n>2时比较cn与an+bn的大小.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-5数列的综合应用(解析版) 题型:填空题
公差d不为0的等差数列{an}的部分项ak1,ak2,ak3,…构成等比数列,且k1=1,k2=2,k3=6,则k4=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-5数列的综合应用(解析版) 题型:选择题
在公差不为零的等差数列{an}中,2a3-a+2a11=0,数列{bn}是等比数列,且b7=a7,则log2(b6b8)的值为( )
A.2 B.4 C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:解答题
已知数列{an}是公差不为0的等差数列,a1=2,且a2,a3,a4+1成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=an+2an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:选择题
设函数f(x)=xm+ax的导函数f′(x)=2x+1,则数列 (n∈N*)的前n项和是( )
(n∈N*)的前n项和是( )
A. B.
B.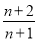 C.
C.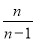 D.
D.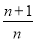
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-2等差数列及其前n项和(解析版) 题型:选择题
已知数列{an},{bn}都是公差为1的等差数列,其首项分别为a1,b1,且a1+b1=5,a1,b1∈N*.设cn=abn(n∈N*),则数列{cn}的前10项和等于( )
A.55 B.70 C.85 D.100
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-4数系的扩充与复数的引入(解析版) 题型:选择题
下面命题:
①0比-i大;
②两个复数互为共轭复数,当且仅当和为实数时成立;
③x+yi=1+i的充要条件为x=y=1;
④如果让实数a与ai对应,那么实数集与纯虚数集一一对应.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com