
设数列{an}满足a1=3,an+1=an2-2nan+2,n=1,2,3,…
(1)求a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);
(2)记Sn为数列{an}的前n项和,试求使得Sn<2n成立的最小正整数n,并给出证明.
(1)a2=5,a3=7,a4=9,猜想an=2n+1
(2)Sn=n2+2n 见解析
【解析】【解析】
(1)a2=5,a3=7,a4=9,猜想an=2n+1.
(2)Sn=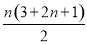 =n2+2n,
=n2+2n,
使得Sn<2n成立的最小正整数n=6.
证明:n≥6(n∈N*)时都有2n>n2+2n.
①n=6时,26>62+2×6,即64>48成立;
②假设n=k(k≥6,k∈N*)时,2k>k2+2k成立,那么2k+1=2·2k>2(k2+2k)=k2+2k+k2+2k>k2+2k+3+2k=(k+1)2+2(k+1),即n=k+1时,不等式成立;
由①、②可得,对于所有的n≥6(n∈N*)
都有2n>n2+2n成立.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:解答题
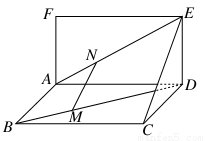
如图,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM=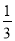 BD,AN=
BD,AN=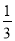 AE.求证:MN∥平面CDE.
AE.求证:MN∥平面CDE.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-3空间点直线平面之间的位置关系(解析版) 题型:解答题
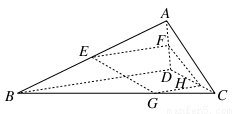
如图,已知在空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且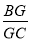 =
=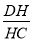 =2.求证:直线EG,FH,AC相交于一点.
=2.求证:直线EG,FH,AC相交于一点.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:填空题
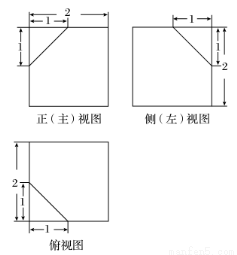
已知某几何体的三视图如图所示,则该几何体的表面积等于________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:选择题
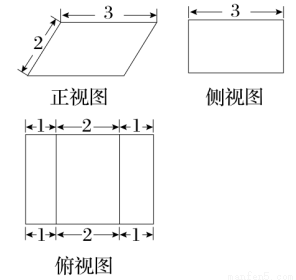
如图,某几何体的正视图是平行四边形,侧视图和俯视图都是矩形,则该几何体的体积为( )
A.6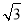 B.9
B.9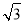 C.8
C.8 D.12
D.12
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:选择题
在数列{an}中,an=1-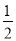 +
+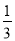 -
-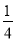 +…+
+…+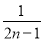 -
-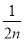 ,则ak+1等于( )
,则ak+1等于( )
A.ak+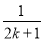 B.ak+
B.ak+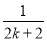 -
-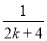
C.ak+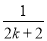 D.ak+
D.ak+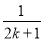 -
-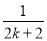
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:填空题
凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有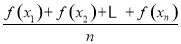 ≤f(
≤f( ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为________.
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:解答题
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求 +
+ +
+ +…+
+…+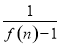 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:解答题
已知a,b,c∈{正实数},且a2+b2=c2,当n∈N,n>2时比较cn与an+bn的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com