练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

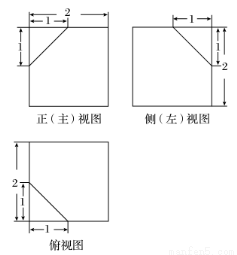
    已知某几何体的三视图如图所示，则该几何体的表面积等于________．

     

     

    【解析】据三视图可知，该几何体是一个正方体(棱长为2)去掉一角(左前上角)而得，直观图如图所示，其中DA＝DB＝DC＝1，

    ∴△ABC是边长为的等边三角形，

    ∴其表面积为

    S＝6×22－3××12＋×()2×

    ＝．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-7立体几何中的向量方法（解析版） 题型：填空题

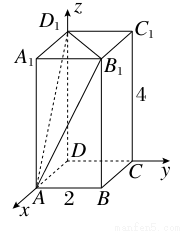
    已知在长方体ABCD－A1B1C1D1中，底面是边长为2的正方形，高为4，则点A1到截面AB1D1的距离是________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-4直线、平面平行的判定及性质（解析版） 题型：填空题

    如图，在正四棱柱ABCD－A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足条件________时，有MN∥平面B1BDD1.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：填空题

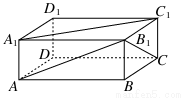
    如图所示，ABCD－A1B1C1D1是长方体，AA1＝a，∠BAB1＝∠B1A1C1＝30°，则AB与A1C1所成的角为________，AA1与B1C所成的角为________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-2空间几何体的表面积和体积（解析版） 题型：解答题

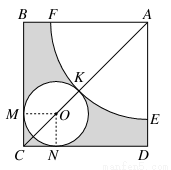
    如图所示，在边长为5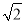＋的长方形ABCD中，以A为圆心画一个扇形，以O为圆心画一个圆，M，N，K为切点，以扇形为圆锥的侧面，以圆O为圆锥底面，围成一个圆锥，求圆锥的全面积与体积．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-2空间几何体的表面积和体积（解析版） 题型：选择题

    一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则该几何体的体积为(　　)

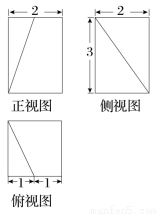
    A．9 B．10 C．11 D．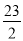

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-7数学归纳法（解析版） 题型：解答题

    设数列{an}满足a1＝3，an＋1＝an2－2nan＋2，n＝1,2,3，…

    (1)求a2，a3，a4的值，并猜想数列{an}的通项公式(不需证明)；

    (2)记Sn为数列{an}的前n项和，试求使得Sn<2n成立的最小正整数n，并给出证明．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：填空题

    请阅读下列材料：若两个正实数a1，a2满足a12＋a22＝1，那么a1＋a2≤.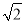

    证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.

    根据上述证明方法，若n个正实数满足a12＋a22＋…＋an2＝1时，你能得到的结论为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-2一元二次不等式及其解法（解析版） 题型：解答题

    设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．

    (1)若m＝－1，n＝2，求不等式F(x)>0的解集；

    (2)若a>0，且0<x<m<n<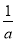，比较f(x)与m的大小．

     

    查看答案和解析>>

    同步练习册答案