
凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有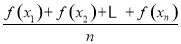 ≤f(
≤f( ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为________.
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为________.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:选择题
如图,在棱长为4的正四面体A-BCD中,M是BC的中点,点P在线段AM上运动(P不与A,M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥平面AMD;②Q点一定在直线DM上;③VC-AMD=4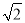 .
.
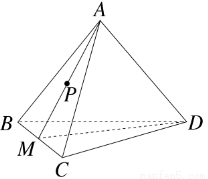
其中正确命题的序号是( )
A.①② B.①③ C.②③ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:解答题
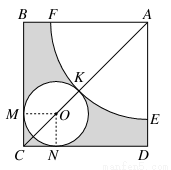
如图所示,在边长为5+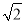 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:解答题
设数列{an}满足a1=3,an+1=an2-2nan+2,n=1,2,3,…
(1)求a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);
(2)记Sn为数列{an}的前n项和,试求使得Sn<2n成立的最小正整数n,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:选择题
平面内有n条直线,最多可将平面分成f(n)个区域,则f(n)的表达式为( )
A. n+1 B. 2n
C.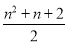 D. n2+n+1
D. n2+n+1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:填空题
请阅读下列材料:若两个正实数a1,a2满足a12+a22=1,那么a1+a2≤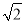 .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤ .
.
根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:选择题
设a,b∈R,则“a+b=1”是“4ab≤1”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:选择题
已知a>0,b>0,若不等式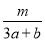 -
- -
- ≤0恒成立,则m的最大值为( )
≤0恒成立,则m的最大值为( )
A.4 B.16 C.9 D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:选择题
若α、β满足-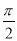 <α<β<
<α<β<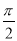 ,则α-β的取值范围是( )
,则α-β的取值范围是( )
A.-π<α-β<π B.-π<α-β<0
C.- <α-β<
<α-β<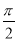 D.-
D.- <α-β<0
<α-β<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com