
���� ��1����������ƽ�еó�tanx����ʽ�ӷ��ӷ�ĸͬ����cosx�ó������
��2���������Ҷ����ó�A�����B�ķ�Χ������f��B�����������Һ������������f��B���ķ�Χ��
��� �⣺��1����$\overrightarrow{m}��\overrightarrow{n}$����$\frac{1}{2}$cosx-$\sqrt{3}$sinx=0����tanx=$\frac{sinx}{cosx}$=$\frac{\sqrt{3}}{6}$��
��$\frac{{\sqrt{3}sinx+cosx}}{{sinx-\sqrt{3}cosx}}$=$\frac{\sqrt{3}tanx+1}{tanx-\sqrt{3}}$=-$\frac{3\sqrt{3}}{2}$��
��2����$\sqrt{3}$c=2asin��A+B��=2asinC����$\frac{c}{sinC}$=$\frac{2a}{\sqrt{3}}$��
��$\frac{c}{sinC}=\frac{a}{sinA}$����sinA=$\frac{\sqrt{3}}{2}$��
�ߡ�ABC����������Σ���A=60�㣬
��$\left\{\begin{array}{l}{0�㣼B��90��}\\{0�㣼120��-B��90��}\end{array}\right.$�����30�㣼B��90�㣬
��f��x��=��$\overrightarrow{m}$+$\overrightarrow{n}$��•$\overrightarrow{m}$=${\overrightarrow{m}}^{2}$+$\overrightarrow{m}•\overrightarrow{n}$=cos2x+1+$\sqrt{3}$sinxcosx+$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x+2=sin��2x+30�㣩+2��
��f��B��=sin��2B+30�㣩+2��
��30�㣼B��90�㣬��90�㣼2B+30�㣼210�㣬
��f��B����f��90�㣩=3��f��B����f��210�㣩=$\frac{3}{2}$��
��f��B����ȡֵ��Χ�ǣ�$\frac{3}{2}$��3����
���� ���⿼����ƽ������ƽ��������Ĺ�ϵ�����Ǻ����Ļ�����ֵ�������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
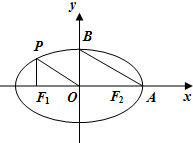 ��ͼ������Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��\;a��b��0\;��$��һ��P��x�������ߣ�����ǡΪ��F1���ֵ�A����Բ��x��������Ľ��㣬��B����Բ��y��������Ľ��㣬��$AB��OP��\;\;|{F_1}A|\;=\sqrt{10}+\sqrt{5}$��
��ͼ������Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��\;a��b��0\;��$��һ��P��x�������ߣ�����ǡΪ��F1���ֵ�A����Բ��x��������Ľ��㣬��B����Բ��y��������Ľ��㣬��$AB��OP��\;\;|{F_1}A|\;=\sqrt{10}+\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�2���ȣ�-2��-$\frac{3}{2}$] | B�� | ��-�ޣ�-2���ȣ�-2��-$\frac{3}{2}$] | C�� | ��-�ޣ�-2�� | D�� | ��-2��-$\frac{3}{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -1 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-1��2+��y+2��2=5 | B�� | ��x-1��2+��y+2��2=20 | C�� | ��x+1��2+��y-2��2=20 | D�� | ��x+1��2+��y-2��2=5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com