
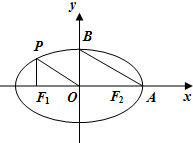
 如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(\;a>b>0\;)$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且$AB∥OP,\;\;|{F_1}A|\;=\sqrt{10}+\sqrt{5}$.
如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(\;a>b>0\;)$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且$AB∥OP,\;\;|{F_1}A|\;=\sqrt{10}+\sqrt{5}$.分析 (Ⅰ) 由题意可知:求得A,B,F1,P点坐标,由kAB=kOP,根据斜率公式,求得b和c的值,根据椭圆的性质,$a=\sqrt{2}c$,由$|{F_1}A|\;=\;a+c=(\sqrt{2}+1)\sqrt{5}$,即可求得a和b的值,求得椭圆方程;
(Ⅱ) 由题意可知:根据中点坐标公式,求得M点坐标,将M代入椭圆方程,即可求得Q的轨迹方程.
解答 解:(Ⅰ) 由题意可知,$A\;(\;a,\;\;0\;),B\;(\;0,\;\;b\;),{F_1}\;(\;-c,\;\;0\;),P\;(\;-c,\;\;\frac{b^2}{a}\;)$,
∵AB∥OP,
∴kAB=kOP,
∴$-\frac{b}{a}=-\frac{b^2}{ac}⇒b=c$,
∵a2=b2+c2,
∴a2=2c2,
∴$a=\sqrt{2}c$,
∴$a+c=(\sqrt{2}+1)\;c$,$|{F_1}A|\;=\;a+c=(\sqrt{2}+1)\sqrt{5}$,
∴$a=\sqrt{10}$,$c=\sqrt{5}$,$b=\sqrt{5}$,
∴椭圆方程为$\frac{x^2}{10}+\frac{y^2}{5}=1$.
(Ⅱ) 设Q(x,y),已知点Q为线段MN中点,N(4,2),则M(2x-4,2y-2),
∵M是椭圆$\frac{x^2}{10}+\frac{y^2}{5}=1$上的动点,
∴$\frac{{{{(2x-4)}^2}}}{10}+\frac{{{{(2y-2)}^2}}}{5}=1$,
即$\frac{{2{{(x-2)}^2}}}{5}+\frac{{4{{(y-1)}^2}}}{5}=1$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,中点坐标公式公式,求动点的轨迹方程,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -6 | C. | -7 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com