
【题目】已知抛物线C:x24py(p为大于2的质数)的焦点为F,过点F且斜率为k(k0)的直线交C于A,B两点,线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG的面积为S.
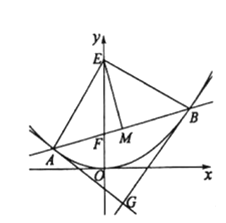
(1)求点G的轨迹方程;
(2)当点G的横坐标为整数时,S是否为整数?若是,请求出所有满足条件的S的值;若不是,请说明理由.
【答案】(1)![]() (2)当G点横坐标为整数时,S不是整数.
(2)当G点横坐标为整数时,S不是整数.
【解析】
(1)先求解导数,得出切线方程,联立方程得出交点G的轨迹方程;
(2)先求解弦长![]() ,再分别求解点
,再分别求解点![]() 到直线
到直线![]() 的距离,表示出四边形的面积,结合点G的横坐标为整数进行判断.
的距离,表示出四边形的面积,结合点G的横坐标为整数进行判断.
(1)设![]() ,则
,则![]() ,
,
抛物线C的方程可化为![]() ,则
,则![]() ,
,
所以曲线C在点A处的切线方程为![]() ,
,
在点B处的切线方程为![]() ,
,
因为两切线均过点G,所以![]() ,
,![]()
所以A,B两点均在直线上![]() ,所以直线AB的方程为
,所以直线AB的方程为![]() ,
,
又因为直线AB过点F(0,p),所以![]() ,即G点轨迹方程为
,即G点轨迹方程为![]() ;
;
(2)设点G(![]() ,
,![]() ),由(1)可知,直线AB的方程为
),由(1)可知,直线AB的方程为![]() ,
,
即![]() ,
,
将直线AB的方程与抛物线联立,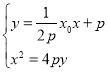 ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,解得
,解得![]() ,
,
因为直线AB的斜率![]() ,所以
,所以![]() ,
,
且![]() ,
,
线段AB的中点为M![]() ,
,
所以直线EM的方程为:![]() ,
,
所以E点坐标为(0,![]() ),
),
直线AB的方程整理得![]() ,
,
则G到AB的距离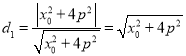 ,
,
则E到AB的距离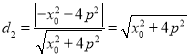 ,
,
所以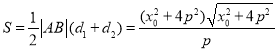 ,
,
设![]() ,因为p是质数,且
,因为p是质数,且![]() 为整数,所以
为整数,所以![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
, 是无理数,不符题意,
是无理数,不符题意,
当![]() 时,
时,![]() ,
,
因为当![]() 时,
时,![]() ,即
,即![]() 是无理数,所以
是无理数,所以![]() 不符题意,
不符题意,
当![]() 时,
时,![]() 是无理数,不符题意,
是无理数,不符题意,
综上,当G点横坐标为整数时,S不是整数.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】对称轴为坐标轴的椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且直线
两点,且直线![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,则当
的斜率依次成等比数列,则当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”.三国时期,吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的锐角![]() ,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
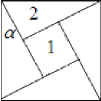
A.30B.40C.50D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2,设勾股形中勾股比为![]() ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
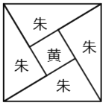
A.134B.866C.300D.188
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地为改善旅游环境进行景点改造.如图,将两条平行观光道l1和l2通过一段抛物线形状的栈道AB连通(道路不计宽度),l1和l2所在直线的距离为0.5(百米),对岸堤岸线l3平行于观光道且与l2相距1.5(百米)(其中A为抛物线的顶点,抛物线的对称轴垂直于l3,且交l3于M),在堤岸线l3上的E,F两处建造建筑物,其中E,F到M的距离为1(百米),且F恰在B的正对岸(即BF⊥l3).
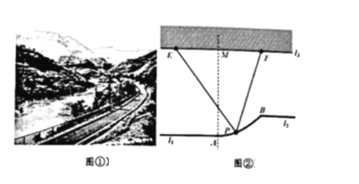
(1)在图②中建立适当的平面直角坐标系,并求栈道AB的方程;
(2)游客(视为点P)在栈道AB的何处时,观测EF的视角(∠EPF)最大?请在(1)的坐标系中,写出观测点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断错误的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
B.已知直线![]()
![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若随机变量![]() 服从二项分布:
服从二项分布: ![]() , 则
, 则![]()
D.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
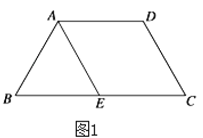
【题目】如图1,等腰梯形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起后如图2,使二面角
折起后如图2,使二面角![]() 成直二面角,设
成直二面角,设![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 的中
的中
点.

(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)判断![]() 能否垂直于平面
能否垂直于平面![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com