练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对称轴为坐标轴的椭圆的焦点为，，在上.

    （1）求椭圆的方程；

    （2）设不过原点的直线与椭圆交于，两点，且直线，，的斜率依次成等比数列，则当的面积为时，求直线的方程.

    【答案】（1）（2）直线的方程为：或

    【解析】

    （1）设椭圆的方程为 ，由椭圆的定义求，进而得到椭圆标准方程；（2）设，.由题意将直线方程与椭圆方程联立，得，，又，，的斜率依次成等比数列，解得，由，到直线的距离， ，解得，得直线方程

    （1）设椭圆的方程为 ，

    由题意可得，又由，得，故，

    椭圆的方程为；

    （2）设，.

    由题意直线的方程为：，

    联立得，

    ，化简，得①

    ②，③

    直线，，的斜率依次成等比数列，，

    ，化简，得

    ，，又，，

    且由①知.

    原点到直线的距离.

    ，解得（负舍）或

    （负舍）.

    直线的方程为：或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2019年底，北京2022年冬奥组委会启动志愿者全球招募，仅一个月内报名人数便突破60万，其中青年学生约有50万人.现从这50万青年学生志愿者中，按男女分层抽样随机选取20人进行英语水平测试，所得成绩(单位:分)统计结果用茎叶图记录如下:

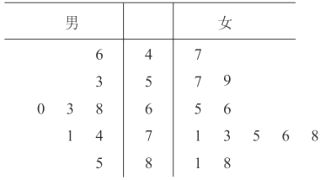
    (Ⅰ)试估计在这50万青年学生志愿者中，英语测试成绩在80分以上的女生人数;

    (Ⅱ)从选出的8名男生中随机抽取2人，记其中测试成绩在70分以上的人数为X，求的分布列和数学期望;

    (Ⅲ)为便于联络，现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000)，并在每组中随机选取个人作为联络员，要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据，以频率作为概率，给出的最小值.(结论不要求证明)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为（为参数），直线的参数方程为（为参数，为直线的倾斜角）.以原点为极点，轴的非负半轴为极轴建立极坐标系，并在两个坐标系下取相同的长度单位.

    （1）当时，求直线的极坐标方程；

    （2）若曲线和直线交于，两点，且，求直线的倾斜角.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为准确把握市场规律，某公司对其所属商品售价进行市场调查和模型分析，发现该商品一年内每件的售价按月近似呈的模型波动（为月份），已知3月份每件售价达到最高90元，直到7月份每件售价变为最低50元.则根据模型可知在10月份每件售价约为_____.（结果保留整数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正三棱柱中，，，分别为，的中点．

    （1）求证：平面；

    （2）求平面与平面所成二面角锐角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    (1)讨论函数的单调性；

    (2)若是函数的两个不同的零点，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】棉花的纤维长度是评价棉花质量的重要指标，某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花，为了评价该品种的棉花质量，在棉花成熟后，分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计，结果如下表：（记纤维长度不低于300的为“长纤维”，其余为“短纤维”）

    纤维长度

    甲地（根数）

    3

    4

    4

    5

    4

    乙地（根数）

    1

    1

    2

    10

    6

    （1）由以上统计数据，填写下面列联表，并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.

    甲地

    乙地

    总计

    长纤维

    短纤维

    总计

    附：（1）；

    （2）临界值表；

    0．10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （2）现从上述40根纤维中，按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测，在这8根纤维中，记乙地“短纤维”的根数为，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，直线与抛物线交于两点.

    （Ⅰ）若，求以为直径的圆被轴所截得的弦长；

    （Ⅱ）分别过点作抛物线的切线，两条切线交于点，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C:x24py（p为大于2的质数）的焦点为F，过点F且斜率为k(k0)的直线交C于A，B两点，线段AB的垂直平分线交y轴于点E，抛物线C在点A，B处的切线相交于点G.记四边形AEBG的面积为S.

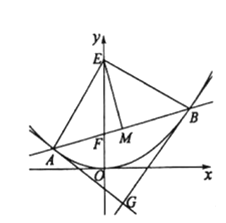
    （1）求点G的轨迹方程；

    （2）当点G的横坐标为整数时，S是否为整数？若是，请求出所有满足条件的S的值；若不是，请说明理由.

    查看答案和解析>>

    同步练习册答案