练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y＝的反函数的定义域是(    )?

    A．(－∞，)∪(，＋∞)?　　　　　　　　　　　　　　   B．(－∞，)∪(，＋∞)?

    C．(－∞，)∪(，＋∞)?　　　　　　　　　　　　　　   D．(－∞，)∪(，＋∞)?

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：数学教研室 题型：022

    如果函数y＝f(x)的反函数是它本身，则y＝f(x)的图象关于直线______对称．其定义域和值域______

    查看答案和解析>>

    科目：高中数学 来源：走向清华北大同步导读·高一数学·上 题型：022

    已知函数y＝f(x)的反函数是(x≥0)，那么y＝f(x)的定义域是________．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    下面的命题正确的有哪些？

    (1)函数y＝f－1(x)的反函数是y＝f(x)；

    (2)如果点M(a，b)在函数y＝f(x)的图象上，且反函数存在，则点(b，a)一定在它的反函数的图象上；

    (3)关于直线y＝x对称的两个图形一定是互为反函数的一对函数的图象；

    (4)因为y＝f(x)的图象与y＝f－1(x)的图象关于y＝x对称，所以y＝f(x)的图象与y＝f－1(x)的图象不可能相交；

    (5)如果y＝f(x)存在反函数，那么f－1(x)的定义域一定是f(x)的值域；

    (6)y＝f(x)在[a，b]上是增函数，那么f－1(x)在[a，b]上也是增函数．

    查看答案和解析>>

    科目：高中数学 来源：安徽省合肥市2007年高三第二次教学质量检测　数学文科 题型：022

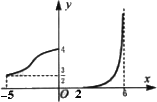
    函数y＝f(x)的图象如图所示，命题：

    ①函数y＝f(x)的定义域是；

    ②函数y＝f(x)的值域是；

    ③函数y＝f(x)在定义域内是增函数；

    ④函数y＝f(x)有反函数．

    其中正确命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学函数专项训练（河北） 题型：解答题

    已知函数f(x)＝()x，

    函数y＝f－1(x)是函数y＝f(x)的反函数．

    (1)若函数y＝f－1(mx2＋mx＋1)的定义域为R，求实数m的取值范围；

    (2)当x∈[－1,1]时，求函数y＝[f(x)]2－2af(x)＋3的最小值g(a)；

    (3)是否存在实数m＞n＞3，使得g(x)的定义域为[n，m]，值域为[n2，m2]？若存在，求出m、n的值；若不存在，请说明理由

     

    查看答案和解析>>

    同步练习册答案