考点:数列的求和
专题:等差数列与等比数列
分析:由已知得数列{a
n}是以a
1=1为首项,4为公差的等差数列,从而S
n=2n
2-n(n∈N
*),
=a
n-2(n-1)=2n-1(n∈N
*),由此S
1+
++…+-(n-1)2=1+3+5+7+…+(2n-1)-(n-1)
2=n
2-(n-1)
2=2n-1.令2n-1=4027,得存在满足条件的自然数n=2014.
解答:
解:∵a
1=1,a
n=
+2(n-1)(n∈N*),
∴S
n=na
n-2n(n-1)(n∈N
*).
当n≥2时,a
n=S
n-S
n-1=na
n-(n-1)a
n-1-4(n-1),即a
n-a
n-1=4,
∴数列{a
n}是以a
1=1为首项,4为公差的等差数列.
于是,a
n=4n-3,S
n=2n
2-n(n∈N
*).
∴
=a
n-2(n-1)=2n-1(n∈N
*),
∵S
1+
++…+-(n-1)2=4027,
∴S
1+
++…+-(n-1)2=1+3+5+7+…+(2n-1)-(n-1)
2=n
2-(n-1)
2=2n-1.
令2n-1=4027,得n=2014,
即存在满足条件的自然数n=2014.
故选:C.
点评:本题考查满足条件的自然数n的求法,是中档题,解题时要认真审题,注意构造法和等差数列的性质的合理运用.



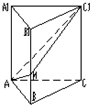 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=