
直线l1和l2的方程分别为A1x+B1y+C1=0和A2x+B2y+C2=0,其中A1、B1不全为0,A2、B2也不全为0,试探究:
(1)当l1∥l2时,直线方程中的系数应满足什么关系?
(2)当l1⊥l2时,直线方程中的系数应满足什么关系?
|
导思:在利用直线方程的一般式判断两直线的位置关系时,可以由系数间的关系直接作出结论,设l1∶A1x+B1y+C1=0,l2∶A2x+B2y+C2=0. (1)l1∥l2 (2)l1与l2相交 (3)l1与l2重合 (4)l1⊥l2 探究:当A1、B1全不为0,A2、B2也全不为0时,对l1∥l2与l1⊥l2可以考查它们的斜率关系.当A1、A2、B1、B2中有等于0的情形时,方程比较简易,易于讨论.想一想,能直接利用斜率间的关系求解吗?答案是:当两条直线的斜率都存在时,则其斜率分别为 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| i |
| c |
| 2 |
| 2 |
| i |
| c |
| 2 |
| c |
| i |
| PE |
| PF |
| 2 |
| EM |
| FN |
| EM |
| FN |
| EF |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当l1∥l2时,两条直线在y轴上的截距明显不同,但哪些量是相等的?
(2)l1⊥l2的条件是什么?
查看答案和解析>>
科目:高中数学 来源:2009年上海市浦东新区高考数学二模试卷(文理合卷)(解析版) 题型:解答题
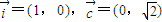 ,若过定点
,若过定点 、以
、以 (λ∈R)为法向量的直线l1与过点
(λ∈R)为法向量的直线l1与过点 以
以 为法向量的直线l2相交于动点P.
为法向量的直线l2相交于动点P. 恒为定值;
恒为定值; 上的两个动点,且
上的两个动点,且 ,试问当|MN|取最小值时,向量
,试问当|MN|取最小值时,向量 与
与 是否平行,并说明理由.
是否平行,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com