【题目】运动会时，高一某班共有28名同学参加比赛，每人至多报两个项目．15人参加游泳，8人参加田径，14人参加球类．同时参加游泳和田径的有3人，同时参加游泳和球类的有3人，则只参加一个项目的有______人．
【答案】19
【解析】
根据15人参加游泳比赛，有8人参加田径比赛，同时参加游泳和田径的有3人，同时参加游泳和球类比赛的有3人，可以求得只参加游泳比赛的人数；再结合总人数即可求得同时参加田径和球类比赛的人数．
解：有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，这三项累加时，比全班人数多算了三部分，
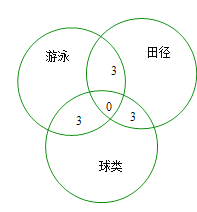
即同时参加游泳比赛和田径比赛的，同时参加游泳比赛和球类比赛的和同时参加田径比赛和球类比赛的重复算了两次，
所以
就是同时参加田径比赛和球类比赛的人数，
所以同时参加田径比赛和球类比赛的有3人．
∵同时参加游泳和田径的有3人，同时参加游泳和球类的有3人，
∴只参加一个项目的有
人，
故答案为：19
期末宝典单元检测分类复习卷系列答案科目：高中数学 来源： 题型：
【题目】已知
、
、
为实数，
，
，记集合
，
，则下列命题为真命题的是（ ）
A.若集合
的元素个数为2，则集合
的元素个数也一定为2
B.若集合的元素个数为2，则集合的元素个数也一定为2
C.若集合的元素个数为3，则集合的元素个数也一定为3
D.若集合的元素个数为3，则集合的元素个数也一定为3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速（单位： 
），现将其分成六组为
， 
， 
， 
， 
， 
后得到如图所示的频率分布直方图.
（1）某小型轿车途经该路段，其速度在
以上的概率是多少？
（2）若对车速在
， 
两组内进一步抽测两辆小型轿车，求至少有一辆小型轿车速度在
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直角梯形
中， 
， 
， 
， 
、
分别是边
、
上的点，且
，沿
将
折起并连接成如图的多面体
，折后
．
（Ⅰ）求证： 
；
（Ⅱ）若折后直线
与平面
所成角
的正弦值是
，求证：平面
平面
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，以坐标原点为极点， 
轴的正半轴为极轴建立极坐标系，已知曲线
的极坐标方程为
，过点
的直线
的参数方程为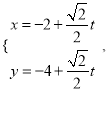
（
为参数），直线
与曲线
相交于
两点．
（Ⅰ）写出曲线
的直角坐标方程和直线
的普通方程；
（Ⅱ）若
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】先后2次抛掷一枚骰子，将得到的点数分别记为
，
.
（1）求直线
与圆
相切的概率；
（2）将，，5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图， 
是圆
的直径，点
是圆
上异于
的点， 
垂直于圆
所在的平面，且
．
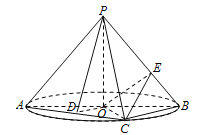
（1）若
为线段
的中点，求证
平面
；
（2）求三棱锥
体积的最大值；
（3）若
，点
在线段
上，求
的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
