
已知A,B,C是椭圆W: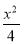 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点.
(1)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积;
(2)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由.
(1)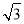 (2)不可能
(2)不可能
【解析】(1)由椭圆W: +y2=1,知B(2,0).
+y2=1,知B(2,0).
因为四边形OABC为菱形,所以AC与OB相互垂直平分,所以可设A(1,t),代入 +y2=1,得t=±
+y2=1,得t=± .∴|AC|=2|t|=
.∴|AC|=2|t|= .
.
因此菱形的面积S=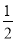 |OB|·|AC|=
|OB|·|AC|=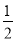 ×2×
×2× =
=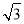 .
.
(2)假设四边形OABC为菱形.
因点B不是W的顶点,且直线AC不过原点,所以可设AC的方程为y=kx+m(k≠0,m≠0).
由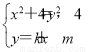 ,消y并整理得(1+4k2)x2+8kmx+4m2-4=0.
,消y并整理得(1+4k2)x2+8kmx+4m2-4=0.
设A(x1,y1),C(x2,y2),则
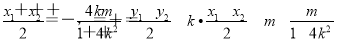 ,
,
∴线段AC中点M  .因为M为AC和OB的交点,∴kOB=-
.因为M为AC和OB的交点,∴kOB=- .
.
又k·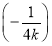 =-
=-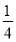 ≠-1,∴AC与OB不垂直.
≠-1,∴AC与OB不垂直.
故四边形OABC不是菱形,这与假设矛盾.
所以,当点B不是W的顶点时,四边形OABC不可能是菱形


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:选择题
已知tan β=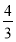 ,sin(α+β)=
,sin(α+β)=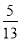 ,其中α,β∈(0,π),则sin α的值为( ).
,其中α,β∈(0,π),则sin α的值为( ).
A.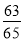 B.
B. 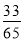 C.
C. 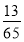 D.
D. 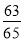 或
或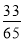
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:解答题
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是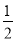 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( ).
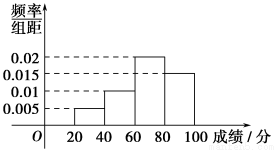
A.45 B.50 C.55 D.60
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
已知椭圆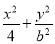 =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( ).
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( ).
A.1 B.2 C.4 D.8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:填空题
椭圆T: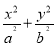 =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=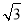 (x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
(x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
“a=b”是“直线y=x+2与圆(x-a)2+(x-b)2=2相切”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:选择题
已知函数f(x)=cos x(x∈(0,2π))有两个不同的零点x1,x2,方程f(x)=m有两个不同的实根x3,x4.若把这四个数按从小到大排列构成等差数列,则实数m的值为( ).
A.-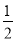 B.
B.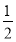 C.
C.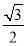 D.-
D.-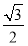
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com