
“a=b”是“直线y=x+2与圆(x-a)2+(x-b)2=2相切”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:解答题
已知A,B,C是椭圆W: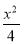 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点.
(1)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积;
(2)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:选择题
已知抛物线y2=4px(p>0)与双曲线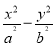 =1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).
=1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).
A.  B.
B. 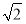 +1 C.
+1 C. 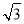 +1 D.
+1 D. 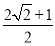
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
若直线l:4x+3y-8=0过圆C:x2+y2-ax=0的圆心且交圆C于A,B两点,O坐标原点,则△OAB的面积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连接DM,则DM与平面PAC所成角的大小是________.
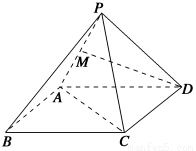
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:选择题
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
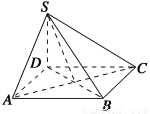
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:填空题
如图,在三棱柱A1B1C1?ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F?ADE的体积为V1,三棱柱A1B1C1?ABC的体积为V2,则V1∶V2=________.
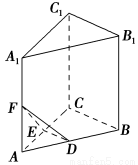
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:填空题
一个圆锥和一个半球有公共底面,如果圆锥的体积和半球的体积相等,则这个圆锥的母线与轴所成角正弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com