
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 时,若直线
时,若直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,函数
时,函数![]() 无极值;当
无极值;当![]() 时,
时, ![]() 有极小值为
有极小值为![]() ,无极大值.
,无极大值.
(2)![]() .
.
【解析】试题分析:(1)求得![]() ,可分
,可分![]() 和
和![]() 两种情况分类讨论,得出函数的单调性,即可求得函数的极值;
两种情况分类讨论,得出函数的单调性,即可求得函数的极值;
(2)当![]() 时,把直线
时,把直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,等价于关于
没有公共点,等价于关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,即关于
上没有实数解,即关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,即
上没有实数解,即![]() 在
在![]() 上没有实数解,令
上没有实数解,令![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与极值,即可求解实数
的单调性与极值,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)![]() 定义域为
定义域为![]() ,
, ![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 为
为![]() 上的增函数,所以函数
上的增函数,所以函数![]() 无极值.
无极值.
②当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递增.
上单调递增.
故![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极小值.
,无极小值.
综上,当![]() 时,函数
时,函数![]() 无极值;
无极值;
当![]() 时,
时, ![]() 有极小值为
有极小值为![]() ,无极大值.
,无极大值.
(2)当![]() 时,
时, ![]() ,
,
直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,等价于关于
没有公共点,等价于关于![]() 的方程
的方程![]()
在![]() 上没有实数解,即关于
上没有实数解,即关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,
上没有实数解,
即![]() 在
在![]() 上没有实数解.
上没有实数解.
令![]() ,则有
,则有![]() .令
.令![]() ,解得
,解得![]() ,
,
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
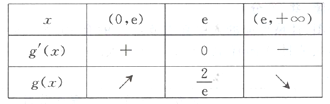
且当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() 的最大值为
的最大值为![]() ;当
;当![]() 时,
时, ![]() ,
,
从而![]() 的取值范围为
的取值范围为![]() .
.
所以当![]() 时,方程
时,方程![]() 无实数解,
无实数解,
解得![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在一次恶劣气候的飞行航程中调查男女乘客在飞机上晕机的情况,共调查了89位乘客,其中男乘客有24人晕机,31人不晕机;女乘客有8人晕机,26人不晕机
(1)根据此材料数据完成如下的2×2列联表;
晕机 | 不晕机 | 总计 | |
男人 | |||
女人 | |||
总计 |
(2)根据列联表,利用下列公式和数据分析,你是否有90%的把握认为在本次飞机飞行中晕机与性别有关?
(3)其中8名晕机的女乘客中有5名是常坐飞机的乘客,另外3名是不常坐飞机的,从这8名乘客中任选3名,这3名乘客不都是常坐飞机的概率是多少?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式: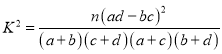 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() ,
,![]() ,…,
,…,![]() 这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计
这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计![]() ,
,![]() ,
,![]() ,
,![]() 这4个球队已经赛过的场数分别为:
这4个球队已经赛过的场数分别为:![]() 队4场,
队4场,![]() 队3场,
队3场, ![]() 队2场,
队2场,![]() 队1场,则
队1场,则![]() 队比赛过的场数为( )
队比赛过的场数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自古以来“民以食为天”,餐饮业作为我国第三产业中的一个支柱产业,一直在社会发展与人民生活中发挥着重要作用.某机构统计了2010~2016年餐饮收入的情况,得到下面的条形图,则下面结论中不正确的是( )

A. 2010~2016年全国餐饮收入逐年增加
B. 2016年全国餐饮收入比2010年翻了一番以上
C. 2010~2016年全国餐饮收入同比增量最多的是2015年
D. 2010~2016年全国餐饮收入同比增量超过3000亿元的年份有3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一劳动节放假,某商场进行一次大型抽奖活动.在一个抽奖盒中放有红、橙、黄、绿、蓝、紫的小球各2个,分别对应1分、2分、3分、4分、5分、6分.从袋中任取3个小球,按3个小球中最大得分的8倍计分,计分在20分到35分之间即为中奖.每个小球被取出的可能性都相等,用![]() 表示取出的3个小球中最大得分,求:
表示取出的3个小球中最大得分,求:
(1)取出的3个小球颜色互不相同的概率;
(2)随机变量![]() 的概率分布和数学期望;
的概率分布和数学期望;
(3)求某人抽奖一次,中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,
, ![]() 的离心率
的离心率![]()
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com