
 如图所示,四边形MNPQ为圆内接四边形,对角线MP与NQ相交于点S,R为MN与QP延长线的交点,且MN=NP,∠MPQ=60°,△MPR为等腰三角形.
如图所示,四边形MNPQ为圆内接四边形,对角线MP与NQ相交于点S,R为MN与QP延长线的交点,且MN=NP,∠MPQ=60°,△MPR为等腰三角形.分析 (Ⅰ)利用等腰三角形的性质,即可求∠PQM的大小;
(Ⅱ)若MN=3,求出MP,PQ,即可求QM的长.
解答 解:(Ⅰ)∵MN=NP,∴∠NMP=∠NPM,
∵△MPR为等腰三角形,PM=PR,∴∠NMP=∠R
∵∠MPQ=60°,
∴∠PMR=∠R=30°,
∴∠PQM=∠MQN+∠NQP=∠MPN+∠NMP=60°;
(Ⅱ)∵MN=NP,
∴∠NPM=30°,
∵∠MPQ=60°,∴∠NPQ=90°,
∴PQ=3tan60°=3$\sqrt{3}$
∵MN=3,
∴MP=2×$3×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∵∠MPQ=60°,
∴QM=3$\sqrt{3}$.
点评 本题考查等腰三角形的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
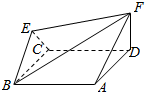 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且FD=$\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且FD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
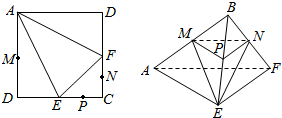 如图,在边长为2的正方形ABCD中,E,F分别为CD,BC的中点,M,N,P分别为AD,CF,CE的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,构成一个三棱锥B-AEF.
如图,在边长为2的正方形ABCD中,E,F分别为CD,BC的中点,M,N,P分别为AD,CF,CE的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,构成一个三棱锥B-AEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
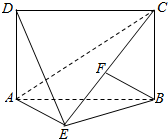 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
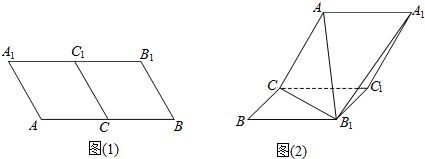
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
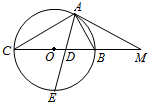 如图所示,MA为圆O的切线,A为切点,割线MC交圆O于B,C两点,MA=6,MB=3,AB=$\sqrt{17}$,∠BAC的角平分线与BC和圆O分别交于点D,E.
如图所示,MA为圆O的切线,A为切点,割线MC交圆O于B,C两点,MA=6,MB=3,AB=$\sqrt{17}$,∠BAC的角平分线与BC和圆O分别交于点D,E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,总有2x≤1 | B. | ?x≤0,总有2x≤1 | ||
| C. | $?{x_0}≤0,使得{2^{x_0}}≤1$ | D. | $?{x_0}>0,使得{2^{x_0}}≤1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com