
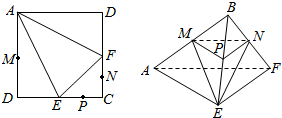
 如图,在边长为2的正方形ABCD中,E,F分别为CD,BC的中点,M,N,P分别为AD,CF,CE的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,构成一个三棱锥B-AEF.
如图,在边长为2的正方形ABCD中,E,F分别为CD,BC的中点,M,N,P分别为AD,CF,CE的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,构成一个三棱锥B-AEF.分析 (1)根据中位线定理得MP∥AE,PN∥EF,故平面MNP∥平面AEF;
(2)把△PNE看做棱锥的底面,则棱锥的高为MB,代入体积公式计算.
解答 证明:(1)∵M,P,分别是AB,BE的中点,∴MP∥AE,
∵AE?平面AEF,MP?平面AEF,
∴MP∥平面AEF,
同理可得:NP∥平面AEF,又∵MP?平面MNP,NP?平面MNP,MP∩NP=P,
∴平面MNP∥平面AEF.
(2)∵P,N是BE,BF的中点,∴S△PNE=$\frac{1}{4}$S△BEF=$\frac{1}{4}×\frac{1}{2}×1×1$=$\frac{1}{8}$.
∵AB⊥BE,AB⊥BF,BE∩BF=B,BE?平面BEF,BF?平面BEF,∴AB⊥平面BEF,
∴三棱锥P-MNE的体积V=$\frac{1}{3}$S△PNE•MB=$\frac{1}{3}×\frac{1}{8}×1$=$\frac{1}{24}$.
点评 本题考查了面面平行的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
总体有编号为01,02,…,19,20的20个个体组成。利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )

A.08 B.07 C.02 D.01
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
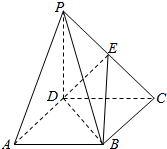 如图,已知四棱锥P-ABCD的底面是矩形,PD⊥平面ABCD,PD=CD,点E是PC的中点,连接DE、BD、BE.
如图,已知四棱锥P-ABCD的底面是矩形,PD⊥平面ABCD,PD=CD,点E是PC的中点,连接DE、BD、BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
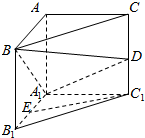 在直三棱柱ABC-A1B1C1中,∠BAC=90°,D,E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
在直三棱柱ABC-A1B1C1中,∠BAC=90°,D,E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
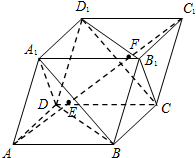 如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$.
如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
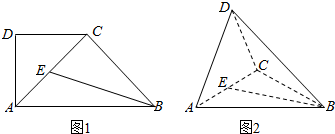 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2,点E为AC中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2,点E为AC中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四边形MNPQ为圆内接四边形,对角线MP与NQ相交于点S,R为MN与QP延长线的交点,且MN=NP,∠MPQ=60°,△MPR为等腰三角形.
如图所示,四边形MNPQ为圆内接四边形,对角线MP与NQ相交于点S,R为MN与QP延长线的交点,且MN=NP,∠MPQ=60°,△MPR为等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com