练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     

    判断二次函数f(x)=ax2+bx+c(a<0)在区间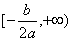上的增减性并依定义给出证明。

     

     

     

     

     

     

     

     

     

    【答案】

     解：f(x)在上是减函数……………………………………………………1分

    设x1,x2∈且x1<x2…………………………………………………………2分

    ∵x1 , x2 ∈  ∴－< x1 +x2<+∞…………………………………………8分

    ∴x1 +x2+ >0，而x1 －x2<0, a<0……………………………………………………10分

    ∴f(x1)－f(x2)>0  即f(x1)>f(x2)

    ∴二次函数f(x)=ax2+bx+c(a<0)在区间上是减函数………………………12分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知二次函数f(x)=ax2+bx+1和g(x)=
    bx-1a2x+2b

    （1）f（x）为偶函数，试判断g（x）的奇偶性；
    （2）若方程g（x）=x有两个不相等的实根，当a＞0时判断f（x）在（-1，1）上的单调性；
    （3）若方程g（x）=x的两实根为x1，x2f（x）=0的两根为x3，x4，求使x3＜x1＜x2＜x4成立的a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f(x)=ax2+bx+1和g(x)=
    bx-1a2x+2b

    （1）f（x）为偶函数，试判断g（x）的奇偶性；
    （2）若方程g（x）=x有两个不相等的实根，当a＞0时判断f（x）在（-1，1）上的单调性；
    （3）当b=2a时，问是否存在x的值，使满足-1≤a≤1且a≠0的任意实数a，不等式f（x）＜4恒成立？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设二次函数f(x)=ax2+bx+c(a、b、c∈R),且f(1) =-,a＞2c＞b.

    (1)判断a、b的符号;

    (2)证明f(x)=0至少有一实根在区间(0,2)内;

    (3)求函数y=f(x)图象被x轴所截弦长的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f(x)＝x2＋(2a－1)x＋1－2a

    (1)判断命题“对于任意的a∈R(R为实数集)，方程f(x)＝1必有实数根”的真假，并写出判断过程；

    (2)若y＝f(x)在区间(－1,0)及(0，)内各有一个零点.求实数a的范围.

    查看答案和解析>>

    同步练习册答案