【题目】已知向量 
=（﹣2，4）， 
=（﹣1，﹣2）．
（1）求 ， 的夹角的余弦值；
（2）若向量 ﹣λ 与2 + 垂直，求λ的值．
【答案】
（1）解：向量 
=（﹣2，4）， 
=（﹣1，﹣2），
∴ =﹣2×（﹣1）+4×（﹣2）=﹣6，
| |= 
=2 
，
| |= 
= ；
∴ ， 夹角的余弦值为
cosθ= 
= 
=﹣ 
；
（2）解：∵ ﹣λ =（﹣2，4）﹣（﹣λ，﹣2λ）=（λ﹣2，2λ+4），
2 + =（﹣4，8）+（﹣1，﹣2）=（﹣5，6）；
又向量 ﹣λ 与2 + 垂直，
∴（ ﹣2λ ）（2 + ）=﹣5（λ﹣2）+6（2λ+4）=0，
解得λ=﹣ 
．
【解析】（1）根据平面向量的数量积与夹角公式，即可求出两向量夹角的余弦值；（2）根据平面向量的坐标运算与两向量垂直，数量积为0，列出方程求出λ的值．
【考点精析】认真审题，首先需要了解数量积表示两个向量的夹角(设
、
都是非零向量，
，
，
是与
的夹角，则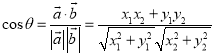
)．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=Asin（ωx+）（A＞0，ω＞0，||＜π）图象的最高点D的坐标为 
，与点D相邻的最低点坐标为 
． （Ⅰ）求函数f（x）的解析式；
（Ⅱ）求满足f（x）=1的实数x的集合．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，PD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=2，PD 
，M为棱PB的中点． （Ⅰ）证明：DM⊥平面PBC；
（Ⅱ）求二面角A﹣DM﹣C的余弦值．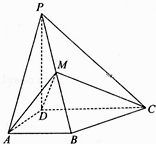
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，已知长方形ABCD中，AB=2，AD=1，E为DC的中点．将△ADE沿AE折起，使得平面ADE⊥平面ABCE．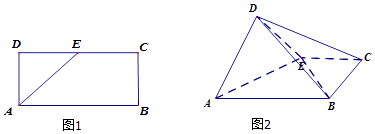 
（1）求证：平面BDE⊥平面ADE
（2）求三棱锥 C﹣BDE的体积
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C的半径为1，圆心C（a，2a﹣4），（其中a＞0），点O（0，0），A（0，3）
（1）若圆C关于直线x﹣y﹣3=0对称，过点A作圆C的切线，求切线的方程；
（2）若圆C上存在点P，使|PA|=|2PO|，求圆心C的横坐标a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义域为R的函数f（x）= 
是奇函数．
（1）求实数a的值，并判断f（x）的单调性（不用证明）；
（2）已知不等式f（logm 
）+f（﹣1）＞0恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在平行四边形ABB1A1中，∠ABB1=60°，AB=4，AA1=2，C，C1分别为AB，A1B1的中点，现把平行四边形ABB1A1沿CC1折起如图2所示，连接B1C，B1A，B1A1 ．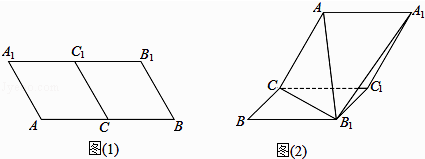 
（1）求证：AB1⊥CC1；
（2）若AB1= 
，求二面角C﹣AB1﹣A1的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市家庭煤气的使用量x（m3）和煤气费f（x）（元） 满足关系f（x）= 
，已知某家庭今年前三个月的煤气费如表：
月份 | 用气量 | 煤气费 |
一月份 | 4m3 | 4 元 |
二月份 | 25m3 | 14 元 |
三月份 | 35m3 | 19 元 |
若四月份该家庭使用了20m3的煤气，则其煤气费为（ ）元．
A.10.5
B.10
C.11.5
D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
