
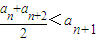 ; ②存在实数M,使得an≤M成立.
; ②存在实数M,使得an≤M成立. (n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;
(n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;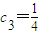 ,
,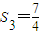 ,证明:数列{Sn}具有“性质m”,并指出M的取值范围;
,证明:数列{Sn}具有“性质m”,并指出M的取值范围; (n∈N*).对于任意的n≥3(n∈N*).
(n∈N*).对于任意的n≥3(n∈N*).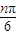 ≤2(n=1,2,3,4,5)判断即可;
≤2(n=1,2,3,4,5)判断即可; 代入S3=
代入S3=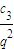 +
+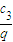 +c3=
+c3= 可求得q,从而可求得c1=1,cn=
可求得q,从而可求得c1=1,cn=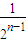 及Sn=2-
及Sn=2-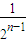 ,分析验证即可;
,分析验证即可;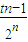 ,可求得dn+1=3t-
,可求得dn+1=3t-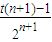 ,dn+2=3t-
,dn+2=3t-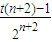 ,利用任意n∈[3,+∞]且n∈N*,数列{dn}具有“性质m”,由dn+dn+2<2dn+1可求得t>1,可判断n≥3时,数列{dn}是单调递增数列,且
,利用任意n∈[3,+∞]且n∈N*,数列{dn}具有“性质m”,由dn+dn+2<2dn+1可求得t>1,可判断n≥3时,数列{dn}是单调递增数列,且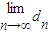 =
=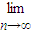 (3t-
(3t-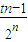 )=3t,从而可求得t≤3,于是有1<t≤3,经检验t=2不合题意,于是得到答案.
)=3t,从而可求得t≤3,于是有1<t≤3,经检验t=2不合题意,于是得到答案.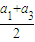 =2=a2,不满足条件①,所以数列{an}不具有“m性质”;…(2分)
=2=a2,不满足条件①,所以数列{an}不具有“m性质”;…(2分)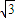 ,b3=2,
,b3=2,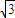 ,b5=1,
,b5=1,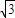 =2b2,
=2b2,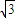 <4=2b3,
<4=2b3,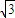 =2b4,所以满足条件①;
=2b4,所以满足条件①;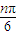 ≤2(n=1,2,3,4,5)满足条件②,所以数列{bn}具有“性质m”.…(4分)
≤2(n=1,2,3,4,5)满足条件②,所以数列{bn}具有“性质m”.…(4分) 代入S3=
代入S3=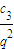 +
+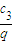 +c3=
+c3= 得,6q2-q-1=0,
得,6q2-q-1=0, 或q=-
或q=- (舍去),…(6分)
(舍去),…(6分)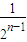 ,
,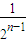 …(7分)
…(7分)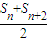 =2-
=2-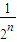 -
-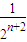 <2-
<2-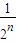 =Sn+1,且Sn<2…(8分)
=Sn+1,且Sn<2…(8分)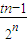 ,则dn+1=3t-
,则dn+1=3t-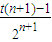 ,dn+2=3t-
,dn+2=3t-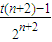 ,
,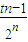 +
+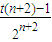 >2×
>2×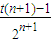 ,化简得,t(n-2)>1…(12分)
,化简得,t(n-2)>1…(12分)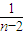 对于任意n∈[3,+∞)且n∈N*恒成立,所以t>1…①…(14分)
对于任意n∈[3,+∞)且n∈N*恒成立,所以t>1…①…(14分)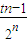 -
-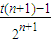 =
=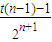 由于n≥3及①,所以dn+1>dn
由于n≥3及①,所以dn+1>dn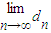 =
=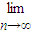 (3t-
(3t-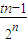 )=3t…(16分)
)=3t…(16分)

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
| 1 |
| 2n+1 |
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+an+2 |
| 2 |
| nπ |
| 6 |
| 1 |
| 4 |
| 7 |
| 4 |
| t (3•2n-n)+1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+an+2 |
| 2 |
| nπ |
| 6 |
| 1 |
| 4 |
| 7 |
| 4 |
| t (3•2n-n)+1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)若数列{an}对于任意的n∈N*都有Sn=2an-n,令f(x)=a1x+a2x2+…+anxn,求函数f(x)在x=1处的导数.
(文)设数列{an}的前n项和为Sn,已知对于任意的n∈N*,都有Sn=2an-n.
(1)求数列{an}的首项a1及递推关系式:an+1=f(an);
(2)先阅读下面的定理:“若数列{an}有递推关系an+1=Aan+B,其中A、B为常数,且A≠1,B≠0,
则数列{an![]() }是以A为公比的等比数列”.请你在(1)的基础上应用本定理,求数列{an}的通项公式;
}是以A为公比的等比数列”.请你在(1)的基础上应用本定理,求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com