
分析 根据不等式恒成立转化为求出z=x2+9y2的最小值即可,作出不等式组对应的平面区域,利用数形结合进行求解即可.
解答 解:作出不等式组对应的平面区域如图:
设z=x2+9y2,则z>0,
即$\frac{{x}^{2}}{z}+\frac{{y}^{2}}{\frac{z}{9}}$=1,则对应的曲线是焦点在x轴上的椭圆,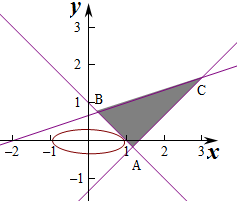
由图象知当直线x+y=1与椭圆相切时,z最小,
将y=1-x代入z=x2+9y2,整理得10x2-18x+9-z=0,
则判别式△=182-4×10(9-z)=0,
解得z=$\frac{9}{10}$,
即z的最小值为$\frac{9}{10}$,
则a≤$\frac{9}{10}$,
则a的最大值为$\frac{9}{10}$,
故答案为:$\frac{9}{10}$
点评 本题主要考查线性规划的应用,根据不等式恒成立,转化为求z=x2+9y2的最小值,利用数形结合结合直线和椭圆的位置关系是解决本题的关键.综合性较强,有一定的难度.


科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,0} | C. | {0,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
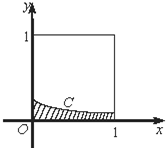 在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值为( )| A. | 1 193 | B. | 1 359 | C. | 2 718 | D. | 3 413 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 某校高三8个班,1班51人,2班53人,3班52人,由此推测各班人数都超过50人 | |
| B. | 由三角形的性质,推测空间四面体的性质 | |
| C. | 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分 | |
| D. | 在数列{an}中,${a_1}=1,{a_n}=\frac{1}{2}({{a_{n-1}}+\frac{1}{{{a_{n-1}}}}})({n≥2})$,通过计算a2,a3,a4推理出{an}的通项公式 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指大气中直径≤2.5微米的颗粒物,其浓度是监测环境空气质量的重要指标.当PM2.5日均值在0~35(单位为微米/立方米,下同)时,空气质量为优,在35~75时空气质量为良,超过75时空气质量为污染.某旅游城市2016年春节7天假期里每天的PM2.5的监测数据如茎叶图所示.
PM2.5是指大气中直径≤2.5微米的颗粒物,其浓度是监测环境空气质量的重要指标.当PM2.5日均值在0~35(单位为微米/立方米,下同)时,空气质量为优,在35~75时空气质量为良,超过75时空气质量为污染.某旅游城市2016年春节7天假期里每天的PM2.5的监测数据如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com