已知正数x,y满足 的最大值为
的最大值为
- A.
- B.
- C.
- D.
B
分析:将原式子变形为
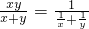
,使用基本不等式求最大值.
解答:解;已知正数x,y满足,x
2+y
2=1,则1=x
2+y
2≥2xy,∴
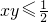
…①
又
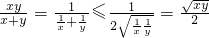
…②
①②联立得
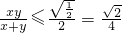
,当且仅当①②两式同取等号,即x=y=

时取到最大值

.
故选B.
点评:本题考查基本不等式的应用,变形是解题的关键,保证等号的取到是难点,也是引发错误的关键.
练习册系列答案
相关习题
科目:高中数学
来源:2014届江西白鹭洲中学高一下学期第二次月考数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:山东省枣庄市2010届高三年级调研考试数学(理科)试题
题型:选择题
查看答案和解析>>
科目:高中数学
来源:山东省枣庄市2010届高三年级调研考试数学(文科)试题
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2010年山东省枣庄市高三调研数学试卷(理科)(解析版)
题型:选择题
已知正数x,y满足

的最大值为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:江苏省高考数学一轮复习单元试卷09:不等式的证明(解析版)
题型:解答题
已知正数x、y满足
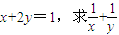
的最小值.
解:∵x+2y=1且x、y>0,
∴
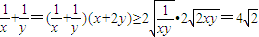
,
∴
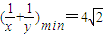
,
判断以上解法是否正确?说明理由;若不正确,请给出正确解法.
查看答案和解析>>

 的最大值为
的最大值为



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案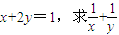 的最小值.
的最小值.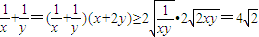 ,
,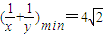 ,
,