
科目:高中数学 来源:不详 题型:解答题
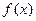 是定义在
是定义在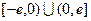 上的奇函数,当
上的奇函数,当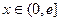 时,
时,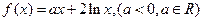
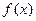 的解析式;
的解析式;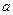 ,使得当
,使得当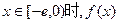 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出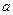 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
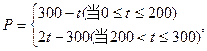 西红柿的种植成本Q与上市时间t满足关系
西红柿的种植成本Q与上市时间t满足关系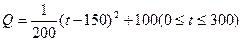 (市场售价与种植成本的单位是:元/100kg,时间单位是:天)。若认定市场售价减去种植成本为纯收益,问:何时上市的西红柿纯收益最大?
(市场售价与种植成本的单位是:元/100kg,时间单位是:天)。若认定市场售价减去种植成本为纯收益,问:何时上市的西红柿纯收益最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
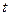 (万元)的关系满足公式P=
(万元)的关系满足公式P=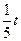 ,Q=
,Q=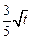 ,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
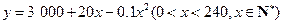 是某产品的总成本
是某产品的总成本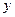 (万元)与产量
(万元)与产量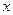 (台)之间的函数关系式,若每台产品
(台)之间的函数关系式,若每台产品 的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是 .
的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com