
【题目】如图,圆锥的轴截面为等腰![]() 为底面圆周上一点。
为底面圆周上一点。
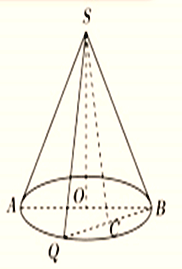
(1)若![]() 的中点为
的中点为![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)如果![]() ,求此圆锥的体积;
,求此圆锥的体积;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() .
.
【答案】(1)证明见解析(2)![]() (3)60°
(3)60°
【解析】
(1)连接![]() 、
、![]() ,由三角形中位线定理可得
,由三角形中位线定理可得![]() ,由圆周角定理我们可得
,由圆周角定理我们可得![]() ,由圆锥的几何特征,可得
,由圆锥的几何特征,可得![]() ,进而由线面垂直的判定定理,得到
,进而由线面垂直的判定定理,得到![]() 平面
平面![]() ,则
,则![]() ,结合
,结合![]() 及线面垂直的判定定理得到
及线面垂直的判定定理得到![]() 平面
平面![]() ;
;
(2)若![]() ,易得
,易得![]() ,又由
,又由![]() ,我们求出圆锥的底面半径
,我们求出圆锥的底面半径![]() 长及圆锥的高
长及圆锥的高![]() ,代入圆锥体积公式,即可得到圆锥的体积;
,代入圆锥体积公式,即可得到圆锥的体积;
(3)作![]() 于点
于点![]() ,由面面垂直的判定定理可得
,由面面垂直的判定定理可得![]() 平面
平面![]() ,作
,作![]() 于点
于点![]() ,连
,连![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,根据二面角
的平面角,根据二面角![]() 的大小为
的大小为![]() ,设
,设![]() ,
,![]() ,进而可求出
,进而可求出![]() 的大小
的大小
(1)如图:
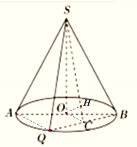
连接![]() 、
、![]() ,因为
,因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() 为圆的直径,所以
为圆的直径,所以![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() .又
.又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)![]()
![]() ,
,![]()
![]() ,
,![]() ,又
,又![]() ,
,![]()
![]() ,
,![]() .
.
(3)作![]() 于点
于点![]() ,
,![]() 平面
平面![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]()
![]() 平面
平面![]() .再作
.再作![]() 于点
于点![]() ,连
,连![]() ,
,![]()
![]() 为二面角
为二面角![]() 的平面角
的平面角
如图:

![]() ,
,![]() .
.
设![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.![]()
![]()
![]() ,解得
,解得![]() ,
,![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列.在欧洲,这个表叫做帕斯卡三角形,帕斯卡(1623-1662)是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,这是我国数学史上的一个伟大成就.如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列![]() ,则此数列前135项的和为( )
,则此数列前135项的和为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年“双节”期间,高速公路车辆较多![]() 某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速
某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速![]() 分成六段:
分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
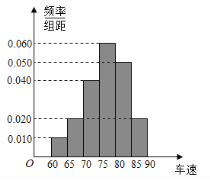
,![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
![]() 某调查公司在采样中,用到的是什么抽样方法?
某调查公司在采样中,用到的是什么抽样方法?
![]() 求这40辆小型车辆车速的众数和中位数的估计值.
求这40辆小型车辆车速的众数和中位数的估计值.
![]() 若从车速在
若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆至少有一辆的概率.
的车辆至少有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
(1)甲不在两端;
(2)甲、乙相邻;
(3)甲、乙、丙三人两两不得相邻;
(4)甲不在排头,乙不在排尾。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(1)求出表中x,y的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
附:K2=![]()
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,过点
,过点![]() 向圆
向圆![]() 引两条切线
引两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则直线
,则直线![]() 的方程为____________;若
的方程为____________;若![]() 为直线
为直线![]() 上一动点,则直线
上一动点,则直线![]() 经过定点__________.
经过定点__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如下表所示:

根据这9年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.243;
作线性相关性检验,求得样本相关系数的绝对值为0.243;
根据后5年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.984.
作线性相关性检验,求得样本相关系数的绝对值为0.984.
(1)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测,方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
附:相关性检验的临界值表:
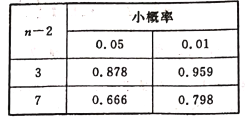
(2)某购物网站同时销售某本畅销书籍的纸质版本和电子书,据统计,在该网站购买该书籍的大量读者中,只购买电子书的读者比例为![]() ,纸质版本和电子书同时购买的读者比例为
,纸质版本和电子书同时购买的读者比例为![]() ,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 轴交于
轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点,记
点,记![]() 与坐标轴围成的三角形
与坐标轴围成的三角形![]() 的面积为
的面积为![]() .
.
(1)若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 、
、![]() 都在正半轴上,求
都在正半轴上,求![]() 的最小值;
的最小值;
(3)写出面积![]() 的取值范围与直线
的取值范围与直线![]() 条数的对应关系.(不需要证明)
条数的对应关系.(不需要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com