
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为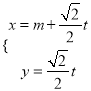 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线上.
在直线上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)设曲线![]() 的内接矩形的周长为
的内接矩形的周长为![]() ,求
,求![]() 的最大值.
的最大值.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinθ,﹣2)与
=(sinθ,﹣2)与 ![]() =(1,cosθ)互相垂直,其中θ∈(0,
=(1,cosθ)互相垂直,其中θ∈(0, ![]() ).
).
(Ⅰ)求sinθ和cosθ的值;
(Ⅱ)若sin(θ﹣φ)= ![]() ,0<φ<
,0<φ< ![]() ,求cosφ的值.
,求cosφ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),且x∈[
),且x∈[ ![]() ,π].
,π].
(1)求 ![]()
![]() 及|
及| ![]() +
+ ![]() |;
|;
(2)求函数f(x)= ![]()
![]() +|
+| ![]() +
+ ![]() |的最大值,并求使函数取得最大值时x的值.
|的最大值,并求使函数取得最大值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A、B两种规格的金属板,每张面积分别为2m2与3m2 . 用A种规格的金属板可造甲种产品3个,乙种产品5个;用B种规格的金属板可造甲、乙两种产品各6个.问A、B两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]()
(1) 求点P的轨迹方程;
(2)设点![]() 在直线x=-3上,且
在直线x=-3上,且![]() .证明过点P且垂直于OQ的直线l过C的左焦点F.
.证明过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com