
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
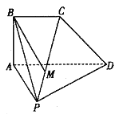
(1)证明:![]() ;
;
(2)设点M在线段PC上,且![]() ,若
,若![]() 的面积为
的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】命题正确的是( )
A.若一个平面内由无穷多个点到另一个平面的距离相等,则这两个平面平行;
B.一个平面内的两条相交直线与另一个平面内的两条相交直线分别垂直,则这两个平面垂直;
C.若一个平面内有3条两两不平行的直线与另一个平面所成角均相等,则这两个平面平行;
D.若两个平面相交,则一个平面内不存在不共线三点到另一个平面距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排6名同学前往4所学校进行演讲,要求甲、乙两同学不能前往同一个学校,每个学校都有人前往,每人只前往一个学校,则满足上述要求的不同安排方案数为________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() .设过点
.设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() 周长为
周长为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点![]() ,证明:当直线
,证明:当直线![]() 变化时,总有TA与
变化时,总有TA与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
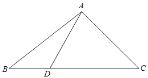
【题目】如图所示,在△ABC中,D是BC边上的一点,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的长和△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13,2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的60%以上,居世界第一位下表截取了2012--2016年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
高铁密度 | 9.75 | 11.49 | 17.14 | 20.66 | 22.92 |
已知高铁密度y与年份代码x之间满足关系式![]() (
(![]() 为大于0的常数)若对
为大于0的常数)若对![]() 两边取自然对数,得到
两边取自然对数,得到![]() ,可以发现
,可以发现![]() 与
与![]() 线性相关.
线性相关.
(1)根据所给数据,求y关于x的回归方程(![]() 保留到小数点后一位);
保留到小数点后一位);
(2)利用(1)的结论,预测到哪一年高铁密度会超过30千米/平方千米.
参考公式设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,
,
则回归方程![]() 的系数:
的系数: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心
,且离心![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,直线
的任意两点,直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,试问当
,试问当![]() 时,直线
时,直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com